Mechanism of osmosis

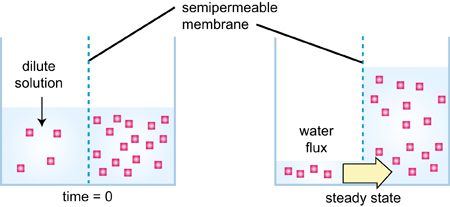
The phenomenon of osmosis may be observed by dividing a container into two equal volumes with a semipermeable membrane. As shown in Fig. 1, the left side contains pure water, the right side contains a dilute glucose solution, and the water levels are equal. Over time, the level on the right rises as water flows from the left to the right side. As the solution level on the right increases, pressure forces water back through the membrane. Eventually, the system equilibrates, such that the rates of the forward and reverse water flow through the membrane are equal and the level on the right stops rising. The osmotic pressure is the pressure required to reach equilibrium (that is, to stop osmosis) and is a characteristic of the solution (Fig. 2).

Fig. 1 Osmosis process. (Credit: McGraw-Hill Education)

Fig. 2 Concept of osmotic pressure. (Credit: McGraw-Hill Education)

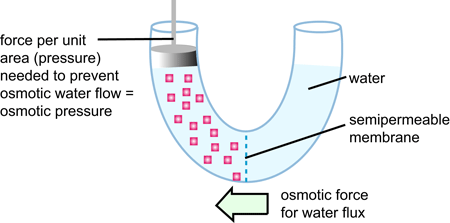
Osmotic pressure

The driving force for osmosis is the decrease in Gibbs free energy accompanying the dilution of the solution by the transfer of solvent to the solution. With G₁⁰ representing the molar free energy of the pure solvent, the molar free energy of solvent in the solution is shown in Eq. (1),

(1)

where R is the molar gas law constant, 8.314 J mole⁻¹ K⁻¹, and a₁ is the solvent activity in the solution. This is conventionally taken as unity for the pure solvent, and in ideal solutions, as the mole fraction, x₁. The pressure that must be applied to the solution phase to increase the solvent free energy to that of the pure solvent is the osmotic pressure, π, of the solution. The rate at which the free energy of a system is changed at a fixed temperature by pressure is given by the basic thermodynamic relationship (2).

(2)

For an incompressible liquid solution, the osmotic pressure is, then, shown in Eq. (3),

(3)

where V₁ is the molar volume of solvent. Equation (3) represents the fundamental relationship between the osmotic pressure and solution thermodynamics. In an ideal solution containing n₁ moles of solvent and n₂ moles of solute, the solvent activity is a₁ = x₁ = n₁/(n₁+n₂). In terms of the solute, the solvent activity is (1 − x₂), where x₂ is the solute mole fraction, n₂/(n₁ + n₂). For dilute solutions, ln a₁ = ln (1 − x₂) ∼ − x₂ since n₁ >> n₂. Then Eq. (3) becomes Eq. (4),

(4)

where n₁ V₁ is replaced by the total volume, V. Equation (4) is recognized as identical in form to the ideal gas law, in which c represents the solute concentration in moles L⁻¹. As applied to osmotic phenomena, Eq. (4) is called the van't Hoff equation. Measurements of osmotic pressure made early in the twentieth century on dilute sucrose solutions using copper ferrocyanide membranes confirm the applicability of (4). For example, a 0.0291 molar aqueous sucrose solution at 15.6°C exhibited an osmotic pressure of 0.684 atm compared with the calculated value of 0.689 atm.

Solution properties reflecting changes in solvent free energy caused by a nonvolatile solute include vapor-pressure lowering, boiling-point elevation, freezing-point depression, as well as osmotic pressure. Of these, the last is the most sensitive to solute concentration. Membrane requirements, however, limit its usefulness in studying solution thermodynamics.

An important application of measuring osmotic pressure is determining a polymer's molar mass. The polymer sample is dissolved in an organic solvent or in a mixture of solvents, and the osmotic pressure is measured using a pretreated cellophane film membrane. An osmometer is used in which the pressure is measured in terms of the height to which liquid rises in a solution cell capillary above that in the surrounding solvent. In accounting for nonideality, Eq. (3) is used in a modified form (5),

(5)

where c^* is the concentration in g/L, and M, the molar mass in g/mole. B and C are correction terms analogous to gas-phase virial coefficients. RT/M is obtained as a limit of π/c^* as c^* approaches zero. The molar mass obtained is a number average of the polymer molar mass spectrum of the sample.

Aside from the inorganic-type membranes, which are formed by deposition of the salt in a porous matrix, membranes suitable for measurements of osmotic pressures in aqueous systems are not available. A number of synthetic polymeric films, which allow the passage of water and small ionic or molecular species, are sufficiently strong to act as selectively permeable membranes in aqueous solutions. These have been successfully used to study, for example, micellar interactions in salt and buffered media. Although the pressures measured are not true osmotic pressures, thermodynamic solute data may be obtained through a redefined G⁰₁ and use of standard Gibbs-Duhem activity relationships. See also: Free energy

Reverse osmosis

Just as the osmotic pressure is that pressure which when applied to the solution phase will prevent the solvent from passing through a semipermeable membrane into the solution, the application of greater pressure will cause solvent to pass from the solution into the pure solvent, or reverse osmosis. Reverse osmosis has long been considered for water purification. Reverse osmosis has long been used as an approach to water desalination and more recently for treating wastewater for reuse. See also: Membrane separations; Wastewater reuse; Water desalination; Water treatment

Francis J. Johnston