Water ship waves

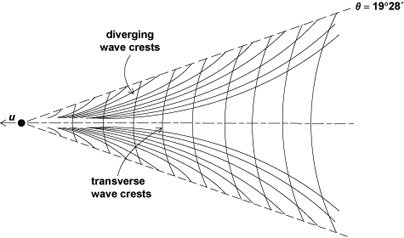
The term ship wave derives from analogy to the pattern of waves behind a moving ship. These waves travel with the ship; that is, they are stationary in a coordinate frame moving with the ship. In relatively deep water, this wave pattern consists of two sets of waves: a transverse wave set, with waves aligned approximately normal to the direction of motion of the ship; and a diverging wave set that appears to extend out radially behind the ship at an angle to the direction of motion of the ship (Fig. 2). This wave pattern was first successfully explained in 1891 by Lord Kelvin (William Thompson) and is therefore often referred to as the Kelvin ship-wave pattern. Kelvin's analysis correctly predicted all the essential features of the observed deep-water ship-wave pattern, namely, the existence of both diverging and transverse wave sets that are confined to a fixed angle or wedge of half-width approximately 19.5°. (A schematic of the pattern of wave crests is shown in Fig. 3.) The maximum wave amplitudes occur along the wedge line where the transverse and diverging waves coalesce, and decrease exponentially away from and outside of the wedge line. The amplitudes also depend on the shape of the ship; wide ships produce larger-amplitude transverse waves, whereas narrow ships produce larger-amplitude diverging waves. The diverging wave length is highly spatially dependent, but the transverse wave length is nearly constant and depends only on the ship speed. Physically, both waves are free-surface gravity waves; that is, gravity is the restoring force for the wave motion. By changing the reference frame to move with the ship, it is apparent that the same wave pattern will be generated for uniform fluid flow moving over an isolated obstacle, such as a rock in a stream.

Fig. 2 Photograph taken by the author of ship-generated waves produced by several small boats in Long Beach, California, harbor.

Fig. 3 Schematic of Kelvin's classical analysis of deep-water ship waves behind a ship (dot) moving at a constant speed U. Diverging and transverse wave patterns are confined to a wedge of half-width θ = 19°28′.

These arguments must be modified somewhat for ships traveling on water of finite depth. In that case, the diverging gravity wave set, similar to the Mach cone in supersonic flow, is still present, because the waves can always align themselves at some angle to remain stationary, but the transverse wave set can only remain stationary if the ship speed is less than the maximum gravity-wave phase speed (that is, U < $\sqrt[\text{2}]{\mathrm{gH}}$, where U is the ship speed, g is gravity, and H is the water depth). Thus, the wave pattern for a fast-moving ship in shallow water (where the Froude number, F = U/$\sqrt[\text{2}]{\mathrm{gH}}$ >1) consists only of diverging waves. In cases where F < 1, both diverging and transverse waves are present but the wedge angle containing them is variable, increasing from 19.5° for F = 0 to 90° for F = 1. Also, the transverse wavelength no longer depends only on ship speed, but now depends on both U and H. All these features can be seen for the various boats moving at different speeds in Fig. 2. Some have only a diverging wave pattern; others have both transverse and diverging waves, and the wedge angle is different for different boats. For example, the very fast moving jet ski in the center-right of Fig. 2 produces only diverging waves and is relatively wide compared to the other slower moving ships.

Atmospheric ship waves

Atmospheric ship waves in the lee of isolated obstacles (also called lee waves) have properties entirely analogous to finite-depth water ship waves. The atmospheric ship-wave pattern is more complicated, in part because the lee waves are generated in a continuously stratified atmosphere, as opposed to a ship wave, where the wave pattern is confined only to regions near the surface. In the atmosphere, the role of finite depth in regulating the ship-wave pattern on the water surface is replaced by the vertical distribution of wind (U) and stability (N, proportional to the vertical temperature gradient) in the vicinity of the obstacle. In particular, transverse waves may or may not exist, depending on the vertical structure of the ratio of the wind to stability (the so-called Scorer parameter, ℓ² = N²/U²) in the vicinity of the obstacle. In general, gravity waves produced by flow over topography can propagate both horizontally and vertically, losing energy and decreasing in amplitude as they propagate away from the obstacle. However, when ℓ² decreases sufficiently rapidly with height, vertical propagation is inhibited and the waves are “trapped” or “ducted” in finite layers. These conditions allow the formation of transverse waves, which decay very slowly downstream from the forcing obstacle. Also analogous to finite-depth water ship waves, atmospheric transverse waves are favored when the flow is over wide-breadth mountain ranges, rather than over isolated narrow-breadth obstacles.

These lee-wave structures may be visible from the ground or from space when the water vapor concentration (humidity) is sufficient to allow cloud formation in the rising parts of the wave pattern. However, lee waves can be present even when the humidity is too low to form clouds in the wave crests. Figure 4 shows an example of a predominately transverse lee wave pattern in dry air as observed in satellite infrared imagery centered on a water-vapor emission band.

Fig. 4 Example of lee waves over Colorado, observed in the water-vapor channel of the MODIS instrument on October 3, 2005, 1945 UTC. (Courtesy Kris Bedka, CIMSS, University of Wisconsin-Madison)

Because of the complex nature of atmospheric temperature and wind structures and terrain forcing, three-dimensional atmospheric ship-wave patterns can be extremely varied. For example, in Fig. 1, even though the meteorology in the vicinity of each island is similar, the wave patterns behind each island have obvious differences, especially in the structure of the diverging wave components. Further, the vertical structure of the atmosphere can be highly variable, leading to the possibility of multiple trapping layers, resulting in different transverse wave amplitudes and wavelengths at different altitudes. In addition, if the wind direction changes with height, the wave pattern may rotate accordingly. The shape of the obstacle and the orientation of the wind relative to the obstacle also affect the wave pattern. If the obstacle height is large enough, or, more precisely, if the internal Froude number F = U/Nh is small enough (where h is the obstacle height), the flow in the lee can become dominated by shed vortices (often called Kármán vortex streets), or turbulent wakes, destroying the coherence of the wave pattern. Figure 5 shows an example of patterns produced by two islands in the Crozet Islands Archipelago in the southern Indian Ocean. The westernmost island is smaller and produces a familiar ship-wave pattern, while the taller island to the east (with a lower internal F ) produces a string of vertically oriented vortices. Another complication is that ship-wave patterns produced by individual obstacles may overlap and interfere (this can be seen in both Figs. 1 and 4). In regions of constructive interference, wave amplitudes may become large enough to initiate wave breaking and turbulence.

Fig. 5 Atmospheric ship-wave pattern and wake vortices behind two islands in the Crozet Islands Archipelago in the southern Indian Ocean, as observed in MODIS visible satellite imagery on November 4, 2004. (NASA, http://visibleearth.nasa.gov)

The ship-wave pattern is generally possible in any system in which the wave propagation is dispersive (that is, the wave speed depends on the wavelength) and there is a point-source disturbance. As discussed above, this is the case for free-surface water ship waves and atmospheric gravity waves forced by flow over isolated obstacles (such as an island or an overshooting convective tower atop a thunderstorm) in the atmosphere and oceans, and for inertio-gravity waves (where rotational effects are significant). It is also the case for lightning-generated “whistlers” (audio-frequency electromagnetic waves that propagate along the Earth's magnetic field lines).

See also: Atmosphere; Froude number; Kármán vortex street; Vortex; Wake flow

Robert Sharman