Reflection angle

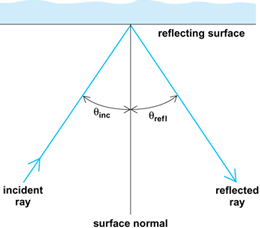
The simplest reflection laws are those that govern plane waves of radiation. The law of reflection concerns the incident and reflected rays (as in the case of a beam from a flashlight striking a mirror) or, more precisely, the wave normals of the incident and reflected rays and the normal to the reflecting surface all lie in one plane, called the plane of incidence, and that the reflection angle θ_refl equals the angle of incidence θ_inc as in Eq. (1)

(1)

[Fig. 2]. The angles θ_inc and θ_refl are measured between the surface normal and the incident and reflected rays, respectively. The surface (in the above example, that of the mirror) is assumed to be smooth, with surface irregularities small compared to the wavelength of the radiation. This results in so-called specular reflection. In contrast, when the surface is rough, the reflection is diffuse. An example of this is the diffuse scattering of light from a screen or from a white wall where light is returned through a whole range of different angles.

Fig. 2 Reflection of electromagnetic radiation from a smooth surface.

Reflectivity

The reflectivity of a surface is a measure of the amount of reflected radiation. It is defined as the ratio of the intensities of the reflected and incident radiation. The reflectivity depends on the angle of incidence, the polarization of the radiation, and the electromagnetic properties of the materials forming the boundary surface. These properties usually change with the wavelength of the radiation. Reflecting materials are divided into two groups: transparent materials and opaque conducting materials. Radiation penetrating a transparent material propagates essentially unattenuated, while radiation penetrating a conducting material is heavily attenuated. Transparent materials are also called dielectrics. In the wavelength range of visible light, typical dielectrics are glass, quartz, and water. Conducting materials are usually metals such as gold, silver, or aluminum, which are good reflectors at almost all wavelengths. See also: Absorption of electromagnetic radiation; Dielectric materials; Polarization of waves

Reflection from metals

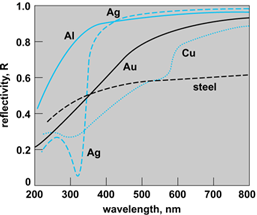
The reflectivity of polished metal surfaces is usually quite high. Silver and aluminum, for example, reflect more than 90% of visible light. The reflectivity of some common metals as a function of wavelength is given in Fig. 3 for normal incidence (θ_inc = 0). The reflectivities vary considerably with wavelength, generally falling off toward the shorter wavelengths, with silver exhibiting a reflection “window” at 320 nanometers. The reflectivity values depend somewhat on the way the metal surface was prepared; for example, whether or not it was polished or was produced by evaporation. The presence of an oxidation layer is also a factor influencing (and usually decreasing) the reflectivity. In ordinary mirrors, the reflecting surface is the interface between metal and glass, which is thus protected from oxidation, dirt, and other forms of deterioration. When it is not permissible to use this protection for technical reasons, one uses “front-surface” mirrors, which are usually coated with evaporated aluminum. The aluminum has a high reflectivity and deteriorates relatively little in the atmosphere. Front-surface mirrors are used in scientific applications such as interferometry and in large reflecting telescopes. See also: Aluminum; Interferometry; Silver; Telescope

Fig. 3 Reflectivity of some common metals for normal incidence as a function of wavelength.

Reflection from dielectrics

The material property that determines the amount of radiation reflected from an interface between two dielectric media is the phase velocity ν of the electromagnetic radiation in the two materials. In optics, one uses as a measure for this velocity the refractive index n of the material, which is defined by Eq. (2)

(2)

as the ratio of the velocity of light c in vacuum and the phase velocity in the material. For visible light, for example, the refractive index of air is about n = 1, the index of water is about n = 1.33, and the index of glass is about n = 1.5. See also: Phase velocity; Refraction of waves

For normal incidence (θ_inc = 0), the reflectivity R of the interface is given by Eq. (3),

(3)

in which the material constants are labeled 1 and 2 as shown in Fig. 4, where the radiation is incident in material 1. The reflectivity of an air-water interface is about 2% (R = 0.02) and that of an air-glass interface about 4% (R = 0.04); the other 98% or 96% are transmitted through the water or glass, respectively.

Fig. 4 Reflection and refraction of electromagnetic radiation at an interface between two dielectric media.

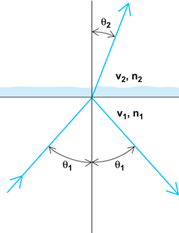
A ray incident upon the interface at an oblique, nonnormal angle θ₁ is deviated as it penetrates material 2 as shown in Fig. 4. This is called refraction, and the refracted angle θ₂ follows from Snell's law of refraction, Eq. (4).

(4)

Again, there is partial reflection, with the reflectivity depending on the angle of incidence θ₁ and the polarization of the radiation. When the electric field is polarized parallel to the plane of incidence, the reflectivity R_∥ is given by Eq. (5),

(5)

and when the electric field is polarized perpendicular to the plane of incidence, the reflectivity R_⊥ is given by Eq. (6).

(6)

These formulas are known as the Fresnel formulas. For unpolarized radiation, in which the electric field varies rapidly in a random, unpredictable manner, the reflectivity $\bar{R}$ is the average of R_∥ and R_⊥. Figure 5 shows R_∥, R_⊥, and $\bar{R}$ for an air-glass interface as a function of angle. The reflectivity approaches 100% at grazing incidence (θ₁ ≈ 90°) for both polarizations. See also: Reflection and transmission coefficients

Fig. 5 Reflectivity as a function of angle of incidence for an air-glass interface.

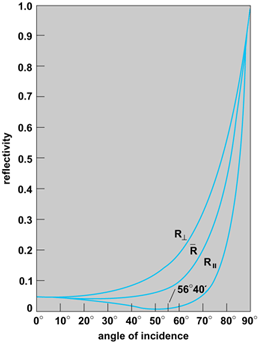
At an angle of about θ₁ = θ_B = 56°, the reflectivity R_∥ assumes zero value. This angle is called Brewster's angle, which is, in general, obtained from formula (7).

(7)

At this angle, which is also called the polarizing angle, only radiation polarized perpendicular to the plane of incidence is reflected.

Total internal reflection

Total reflection, that is, reflection of 100% of the incident radiation, occurs at the interface of two dielectrics when the radiation is incident in the denser medium, that is, when n₁ > n₂ and when the angle of incidence θ₁ is larger than the critical angle θ₀ given by Eq. (8).

(8)

Total internal reflection can be observed, for example, by a submerged diver looking up at the water-air interface for which the critical angle is about θ₀ = 49°. For a glass-air interface the critical angle is approximately θ₀ = 42°.

Selective reflection from crystals

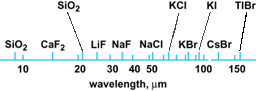
The discussion of reflection from dielectrics to this point has been concerned with reflectivity of nonabsorbing media far removed from absorption bands. These bands are located in the spectral regions where the frequency of the radiation corresponds to a resonance frequency of the atoms, molecules, or crystal lattice of the medium. Because this radiation is strongly absorbed, it is also strongly reflected. The metallic sheen of dye crystals, which have very strong absorption bands in the visible spectrum, is caused by selective reflection. Crystalline solids such as rocksalt or quartz, the lattices of which are built up of atoms bearing net electric charges, show strong selective reflection in the infrared region at wavelengths near those of the strong absorption bands associated with lattice vibrations in the crystal. By reflecting an infrared beam several times from such a material, highly monochromatic radiation can be obtained at the specific wavelengths. These monochromatic beams are referred to as residual rays or reststrahlen. Figure 6 shows residual rays for some crystals. See also: Ionic crystals

Fig. 6 Residual rays for various crystals.

Antireflection coatings

Thin films of antireflective materials are often used to coat surfaces of optical equipment and devices, such as eyeglasses, photographic lenses, and screens, in order to reduce undesired reflections. To minimize reflection, the refractive index n_f of this film should be the geometric mean of the indices n₁ and n₂ of the incident and refracting media, Eq. (9),

(9)

and the film thickness d_f should be equal to a quarter of the wavelength of light in the film material, that is, it should satisfy Eq. (10),

(10)

where λ is the vacuum wavelength of the light for which the reflectivity of the surface is minimized. Such a film is called a quarter-wave layer. Materials such as magnesium fluoride with an index of n = 1.38 are used for antireflection coatings, which reduce the reflectivity to less than 0.1% on certain materials.

High-reflectivity multilayers

A series of dielectric quarter-wave layers of alternating high and low refractive index can be used to produce reflectors of high reflectivity at a specified wavelength. This is called a quarter-wave stack. The high reflectivity is due to an interference effect. Stacks with about 20 layers are used to make reflectors with reflectives higher than 99%. Mirrors such as these are used for the construction of laser resonators. Multilayer coatings are also used to enhance the reflectivity of metals such as aluminum. About four quarter-wave layers can enhance the metal reflectivity to values better than 99%. See also: Albedo; Geometrical optics; Interference filters; Mirror optics; Reflection of sound

Herwig Kogelnik