Surface energy

In the body of a liquid, the time-average force exerted on any given molecule by its neighbors is zero. Even though such a molecule may undergo diffusive displacements because of random collisions with other molecules, no directed forces on it are of long duration. It is equally likely to be momentarily displaced in one direction as in any other. The situation is quite different at the surface of a liquid, because for molecules at the surface, there exist no molecules beyond the free surface to counteract the forces of attraction exerted by molecules in the interior. As a result, molecules at the surface of a liquid experience a net attraction toward the interior of a drop and are therefore pulled toward the interior. The centrally directed “contracting” force is known as surface tension. The surface tension force causes the surface to contract spontaneously, minimizing both the surface free energy and the surface area; and this causes liquid droplets to assume a spherical shape.

From a macroscopic point of view, surface tension may be regarded either as a force exerted normally to a unit length in the surface or as the work that must be expended on the liquid to increase its area by unity. Accordingly, surface tension is expressed in SI units of newtons per meter, N/m (commonly reported as mN/m) or joules per square meter, J/m² (commonly reported as mJ/m²). From a microscopic point of view, the surface tension (or its equivalent, surface energy) is the reversible isothermal work that must be done in bringing molecules from the interior of the liquid to the surface and creating a unit of new surface area.

Most liquids have surface tensions of 10–40 mN/m at room temperature, although water has a higher value of about 72.8 mN/m (at 20°C) and mercury has a much higher value of about 484 mN/m (at 20°C). This shows, for example, that mercury has a much greater cohesive energy (greater attraction between its molecules) than does water. Condensed gases such as helium and nitrogen have quite low surface tensions at about 0.098 mN/m (at −269°C) and about 6.2 mN/m (at −183°C), respectively. Liquid metals have large surface tensions by comparison, such as mercury as noted above and liquid copper at about 1103 mN/m (at 1131°C). In all cases, small but significant differences in the surface tensions of liquids depend on the composition of the vapor phase.

The foregoing refers to a liquid surface in the presence of a gas. Where a liquid surface is in contact with a second, immiscible liquid, the same principles apply. There will still be an imbalance of forces at the surface between the liquids (which is then referred to as an interface), and the interface will still curve to balance the interfacial free energy and minimize the interfacial area. The contracting force at the interface between two immiscible liquids is termed interfacial tension.

Wettability

In a three-phase system in which a liquid is in contact with a gas (or with an immiscible liquid) and also in contact with a solid surface, there will be imbalances of forces at three different surfaces (interfaces). As a result, such things as curvature and minimization of surface free energies are more complicated. An important practical question in such systems is whether the liquid will spread over the solid surface (wetting) or will tend to roll up into a droplet (nonwetting). In the wetting or nonwetting of a solid by a liquid, in the presence of a gas or vapor phase, the principal criterion employed is the contact angle between the solid and the liquid (measured through the liquid, and at the junction of the solid, liquid, and vapor phases) [Fig. 2]. A liquid is completely wetted when the contact angle θ = 0°, is completely nonwetted for θ = 180°, and is partially wetted for intermediate values. In practical applications, this is interpreted somewhat more loosely, and a liquid is frequently said to “wet” a solid if the contact angle θ lies between 0 and 90°, and not to wet the solid if the contact angle is > 90°. Also, values larger than about 140° are not normally encountered in practice, so the practical range of contact angles for nonwetting is more like 90° to 140°.

Fig. 2 Contact angle. (a) Liquid wets solid. (b) Liquid does not wet solid.

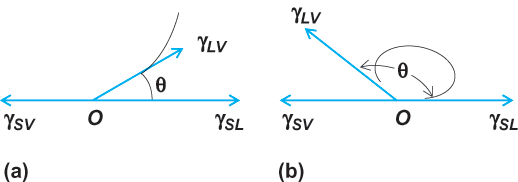
The three phases in the above example also have three interfaces (Fig. 2) and three corresponding interfacial tensions: γ_SL, γ_SV, and γ_LV. The subscripts S, L, and V refer to solid, liquid, and vapor. At equilibrium, a balance of interfacial tensions exists at the three-phase contact line, which is shown in Fig. 2 as point 0. This equilibrium is expressed by Young's equation (1).

(1)

Capillarity

Liquids that wet the walls of fine capillary tubes rise to a height that depends on the tube radius, the surface tension, the liquid density, and the contact angle. In Fig. 3, a liquid of density ρ is shown as having risen to a height h in a capillary whose radius is r. A balance exists between the force exerted by gravity on the mass of liquid raised in the capillary and the opposing force caused by surface tension. The former is πr² hρg, whereas the latter is 2πrγ, assuming the contact angle to be zero and ignoring the mass of the crown of the meniscus. As an approximation, h = 2γ/rρg, showing that the capillary rise varies inversely with the tube radius and the liquid density. Liquids that do not wet the capillary walls, such as mercury in a glass tube, are depressed in height according to the same equation.

Fig. 3 Rise of liquid in capillary tube.

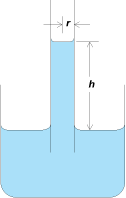
Capillarity is important in more than just vertical tubes. The same principles influence the flow of water in underground rock and soil environments, and the flow of oil and water in underground petroleum reservoirs. In the latter case, the pores in water-wetting (low-θ) rock will tend to have more water in their larger pores, which will tend to contain the oil. This phenomenon and the ability to change this situation by changing the surface (interfacial) tension is exploited in most enhanced oil recovery processes.

Vapor pressure

The shape of the free surface of a liquid in a vessel is only an approximation to a plane. In narrow tubes the meniscus of a liquid is concave upward if the liquid wets the tube and, conversely, convex upward if it does not wet the tube. A pressure difference exists between the concave and convex sides of the surface, with the excess pressure on the concave side over the convex side being given by Eq. (2),

(2)

where r₁ and r₂ are the principal radii of curvature of the surface. The same equation applies for a bubble of gas within a liquid, with the consequence that the vapor pressure p is larger for small bubbles according to Eq. (3),

(3)

where p_o is the vapor pressure over a liquid surface of infinite radius, r is the gas constant, and M is the molar mass. See also: Vapor pressure

Applications

Surface and interfacial tensions can have a strong influence on important phenomena in everyday life, health, and industrial processes. As a result, many chemicals and techniques have been developed for modifying surface and interfacial tensions. Soaps, detergents, and other surfactants of many kinds can be applied to modify the surface tension of water, thereby stabilizing or destabilizing the formation of small bubbles of air, foams, or liquid aerosols; to modify the interfacial tension between oil and water, thereby stabilizing or destabilizing the formation of emulsions; and to raise or lower the interfacial tension between solid surfaces and water so that specific solids are more (or less) readily wetted, and specific particles are more (or less) easily floated. See also: Interface of phases; Surfactant

Laurier L. Schramm