Direction and magnitude

As shown in the example in Fig. 1, a particle moving in the x-y plane with position r and (linear) momentum p has angular momentum L in the z-direction, perpendicular to both r and p. As with any vector cross-product, the direction of the angular momentum in relation, can be determined using the right-hand rule. If the fingers of the right hand are extended straight in the direction of r and curled toward p, the extended thumb points in the direction of L. The magnitude of the angular momentum vector is given by:

(2)

Fig. 1 (a) A particle moving in the x-y plane with position vector r, and linear momentum p has angular momentum parallel to the z-axis. (b) For two generic vectors u and v, the right-hand rule is used to determine the direction of the vector cross-product, $\text{u × v}$.

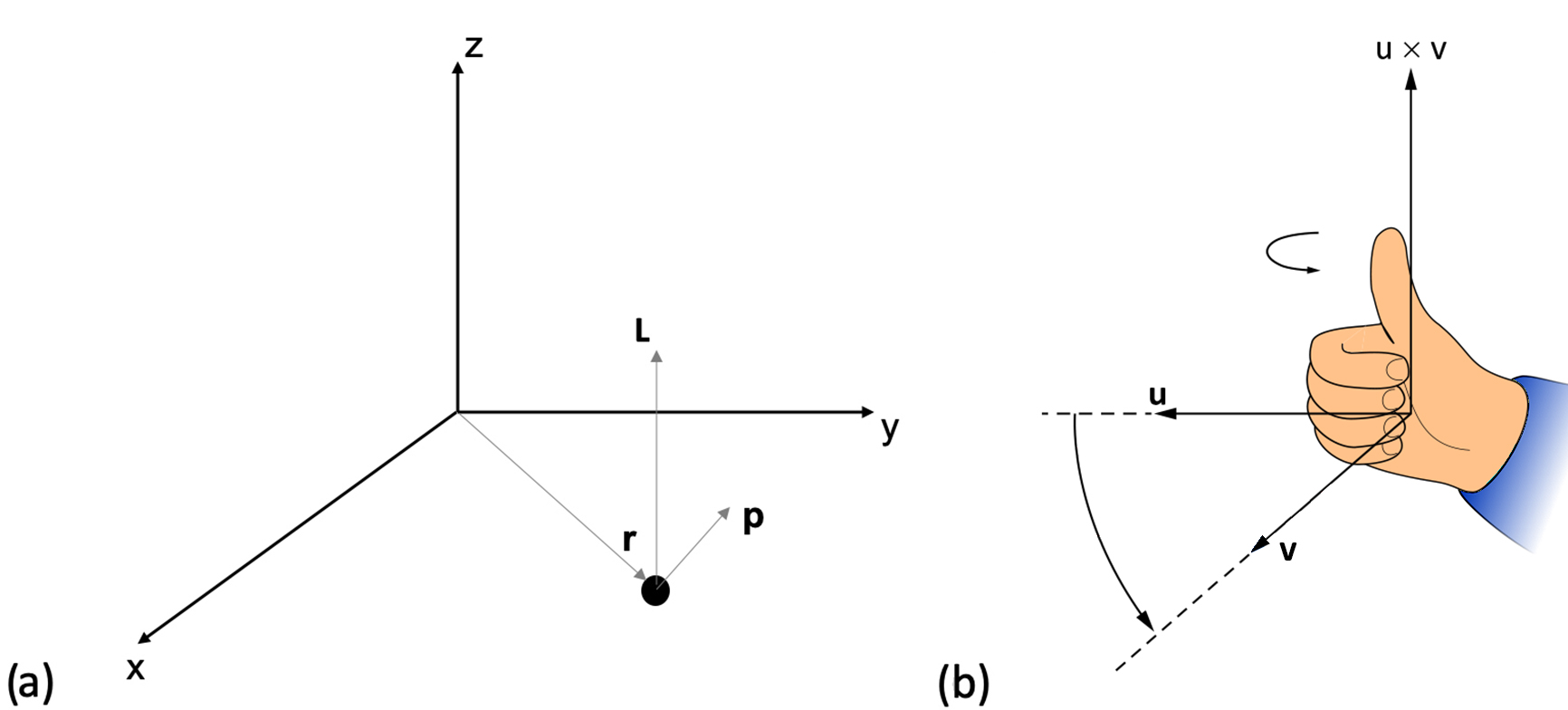
where Θ is the angle made by r and p, and L, r, and p, are the magnitudes of L, r, and p, respectively. Angular momentum is zero when r and p vectors are parallel or anti-parallel (sin Θ = Θ)and maximal when r and p are perpendicular.

Rigid bodies

For a rigid body undergoing rotation, the angular momentum can be defined in terms of the body's moment of inertia I about some axis of motion. The rigid body can be thought of as the summation of many point particles of mass $m{}_i$ at a distance of $r{}_i$ from the object's axis of rotation, so that the moment of inertia for that particular axis of rotation can be written as:

(3)

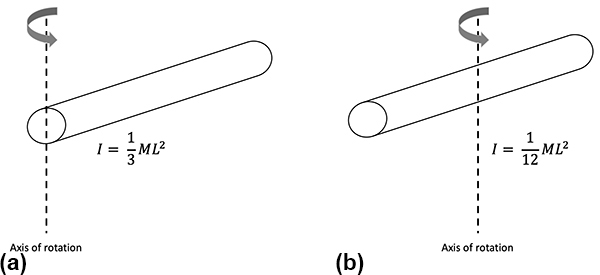
To directly calculate the moment of inertia for any given object, it is more practical to replace the summation in equation (3) by an integral expression. In practice, however, the moments of inertia for standard geometric objects rotating about various axes can usually be found in a table. For example, as shown in Fig. 2, a thin rigid rod with mass M and length L rotating about one end has moment of inertia I = $\raisebox{1ex}{$\text{1}$}\!\left/ \!\raisebox{-1ex}{$\text{3}$}\right.$ ML². The same rod, if rotating about its center, has moment of inertia I = $\raisebox{1ex}{$\text{1}$}\!\left/ \!\raisebox{-1ex}{$\text{12}$}\right.$ ML². Note that the moment of inertia is higher for the same object when rotated in such a way that more of its mass is farther from the axis of rotation. More generally, an object's rotational inertia can be written as an inertia tensor which contains information about all moments of inertia for that object with respect to a given point in space. See also: Moment of inertia

Fig. 2 The moment of inertia for a thin rod with mass M and length L is I = $\raisebox{1ex}{$\text{1}$}\!\left/ \!\raisebox{-1ex}{$\text{3}$}\right.$ ML² if rotating on its end (a), but is I = $\raisebox{1ex}{$\text{1}$}\!\left/ \!\raisebox{-1ex}{$\text{12}$}\right.$ ML² if rotating about its center (b). (Credit: Jonathan Celli)

For an object undergoing a rotation such that it has moment of inertia I, its angular momentum can be written as equation (4):

(4)

where ω is the angular velocity of the object. Written in this form, it is clear that angular momentum is a rotational analog of linear momentum where I is analogous to m and ω is analogous to v.

Torque and angular momentum

For a force F applied at a point given by position vector r, the torque τ is defined as the vector cross-product of r and F in equation (5):

(5)

Just as Newton's Second Law can be written in terms of change in linear momentum as F = $\raisebox{1ex}{$\mathrm{dp}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{dt}$}\right.$, torque can be related to change in angular momentum as equation (6):

(6)

It follows from equation (6) that torque is required to cause change in rotational motion resulting in either increase, decrease, or change in direction of the angular momentum. For example, a torque applied to the pedals makes a bicycle wheel start spinning. Once the bicycle wheel is spinning, it has an angular momentum perpendicular to the plane of the wheel. In order to make the wheel tilt and change the direction of the angular momentum, a torque would have to be applied. This is why a bicycle stays upright more stably when it is in motion and the wheels are spinning, compared to when it is at rest and the wheels are not spinning. See also: Motion; Torque

Conservation of angular momentum

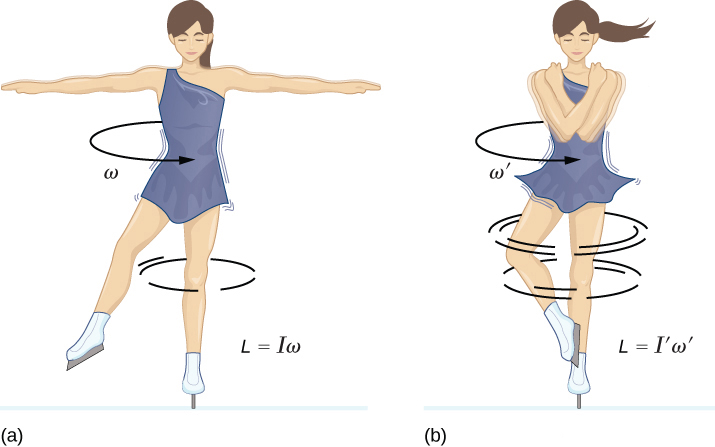
Like linear momentum, angular momentum is a conserved quantity. In the absence of any external torque acting on a closed system, the total angular momentum of that system is conserved. A familiar example of this is shown in Fig. 3. The spinning figure skater comprises a closed system. When her arms are out to the side, more of her mass is distributed farther from the axis of rotation, and therefore her moment of inertia I is higher relative to when she pulls in her arms. Because angular momentum is conserved, her angular velocity, τ, must increase to compensate for the decrease in I when she pulls in her arms. Along with the conservation of energy and linear momentum, the conservation of angular momentum is an essential and fundamental principle in understanding the physics of motion. See also: Conservation of momentum

Fig. 3 Conservation of angular momentum of a spinning figure skater (a). When her arms are pulled in (b), her moment of inertia I decreases and angular velocity τ increases. [Credit: OpenStax University Physics/Attribution 4.0 International (CC BY 4.0)]

In quantum mechanics

The orbital angular momentum operator L in quantum mechanics is defined as the vector cross-product of r and p, analogous to the classical case (Equation 1), but where r and p represent instead the quantum mechanical position and momentum operators, respectively. Elementary particles also carry intrinsic angular momentum in the form of a quantity called spin. Although particles are not physically rotating about their central axis as the name suggests, there is nevertheless this intrinsic form of angular momentum that has been shown to be separate from orbital angular momentum. The total angular momentum operator in quantum mechanics, J, is the sum of the orbital, L, and spin, S, angular momentum operators in equation (7):

(7)

The total angular momentum J is conserved. The quantization of angular momentum plays a critical role in explaining the structure of matter at the atomic and molecular level. See also: Atomic structure and spectra; Elementary particle; Matter; Molecular structure and spectra; Quantum mechanics, Spin

Jonathan Celli