Key Concepts
A branch of physical chemistry that measures the rates of chemical reactions, describes them in terms of elementary steps, and understands them in terms of the fundamental interactions between molecules.
Reaction kinetics
Although the ultimate state of a chemical system is specified by thermodynamics, the time required to reach that equilibrium state is highly dependent upon the reaction. For example, diamonds are thermodynamically unstable with respect to graphite, but the rate of transformation of diamonds to graphite is negligible. As a consequence, determining the rate of chemical reactions has proved to be important for practical reasons. Rate studies have also yielded fundamental information about the details of the nuclear rearrangements which constitute the chemical reaction.
Traditional chemical kinetic investigations of the reaction between species X and Y to form Z and W, reaction (1), sought a rate of the form given in Eq. (2),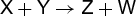 (1)
(1)
where d[Z]/dt is the rate of appearance of product Z, f is some function of concentrations of X, Y, Z, and W which are themselves functions of time, and k is the rate constant. Chemical reactions are incredibly diverse, and often the function f is quite complicated, even for seemingly simple reactions such as that in which hydrogen and bromine combine directly to form hydrogen bromide (HBr). This is an example of a complex reaction which proceeds through a sequence of simpler reactions, called elementary reactions. For reaction (3d), the sequence of elementary reactions is a chain mechanism known to involve a series of steps, reactions (3a)–(3c).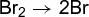 (3a)
(3a)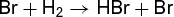 (3b)
(3b)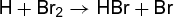 (3c)
(3c)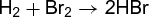 (3d)
(3d)
This sequence of elementary reactions was formerly known as the reaction mechanism, but in the chemical dynamical sense the word mechanism is reserved to mean the detailed motion of the nuclei during a collision.
Bimolecular processes
An elementary reaction is considered to occur exactly as written. Reaction (3b) is assumed to occur when a bromine atom hits a hydrogen molecule. The products of the collision are a hydrogen bromide molecule and a hydrogen atom. On the other hand, the overall reaction is a sequence of these elementary steps and on a molecular basis does not occur as reaction (3d) is written. With few exceptions, the rate law for an elementary reaction A + B → C + D is given by d[C]/dt = k[A][B]. The order (sum of the exponents of the concentrations) is two, which is expected if the reaction is bimolecular (requires only species A to collide with species B). The rate constant k for such a reaction depends very strongly on temperature, and is usually expressed as k = ZABρ exp(−Ea /RT). ZAB is the frequency of collision between A and B calculated from molecular diameters and temperature; ρ is an empirically determined steric factor which arises because only collisions with the proper orientation of reagents will be effective; and Ea, the experimentally determined activation energy, apparently reflects the need to overcome repulsive forces before the reagents can get close enough to react.
Unimolecular processes
In some instances, especially for decompositions, AB → A + B, the elementary reaction step is first-order, Eq. (4),
which means that the reaction is unimolecular. The species AB does not spontaneously dissociate; it must first be given some critical amount of energy, usually through collisions, to form an excited species AB*. It is the species AB* which decomposes unimolecularly.
Relaxation methods
Considerable use has been made of perturbation techniques to measure rates and determine mechanisms of rapid chemical reactions. These methods provide measurements of chemical reaction rates by displacing equilibria. In situations where the reaction of interest occurs in a system at equilibrium, perturbation techniques called relaxation methods have been found most effective for determining reaction rate constants.
A chemical system at equilibrium is one in which the rate of a forward reaction is exactly balanced by the rate of the corresponding back reaction. Examples are chemical reactions occurring in liquid solutions, such as the familiar equilibrium in pure water, shown in reaction (5). The molar equilibrium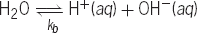 (5)
(5)
constant at 25°C (77°F) is given by Eq. (6),
where bracketed quantities indicate molar concentrations. It arises naturally from the equality of forward and backward reaction rates, Eq. (7). Here kf and kb
are the respective rate constants that depend on temperature but not concentrations. Furthermore, the combination of Eqs. (6) and (7) gives rise to Eq. (8).
Thus a reasonable question might be what the numerical values of kf in units of s−1 and kh in units of dm3 mol−1 s−1 must be to satisfy Eqs. (6) through (8) in water at room temperature. Stated another way, when a liter of 1 M hydrochloric acid is poured into a liter of 1 M sodium hydroxide (with considerable hazardous sputtering), how rapidly do the hydronium ions, H+(aq), react with hydroxide ions, OH−(aq), to produce a warm 0.5 M aqueous solution of sodium chloride? Turbulent mixing techniques are insufficiently fast (mixing time of the order of 1 ms) for this particular reaction to occur outside the mixing chamber. The relaxation techniques were conceived by M. Eigen, who accepted the implied challenge of measuring the rates of seemingly immeasurably fast reactions. See also: Ultrafast molecular processes
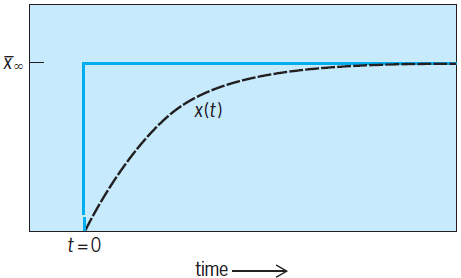
The essence of any of the relaxation methods is the perturbation of a chemical equilibrium (by a small change in temperature, pressure, electric-field intensity, or solvent composition) in so sudden a fashion that the chemical system, in seeking to again achieve equilibrium, is forced by the comparative slowness of the chemical reactions to lag behind the perturbation (Fig. 1).
Temperature jump
Reaction (5) has a nonzero standard enthalpy change, ΔH°, associated with it, so that a small increase in the temperature of the water (H2O) requires the concentrations of hydrogen ions [H+] and hydroxide ions [OH−] to increase slightly, and [H2O] to decrease correspondingly, for chemical equilibrium to be restored at the new higher temperature. Thus a small sample cell containing a very pure sample of water may be made one arm of a Wheatstone conductance bridge, and further configured so that a pulse of energy from a microwave source (or infrared laser of appropriate wavelength) is dissipated in the sample liquid. The resulting rise in temperature of about 2°C (3.6°F) will produce a small increase in conductance that will have an exponential shape and a time constant or relaxation time τ ≃ 27 microseconds; τ is the time required for the signal amplitude to drop to 1/e = 1/2.718 of its initial value, where e is the base of natural logarithms.
In pure water at 25°C (77°F), [H+] = [OH−] = 10−7 M, and for small perturbations, the value for τ is given by Eq. (9), from which it follows
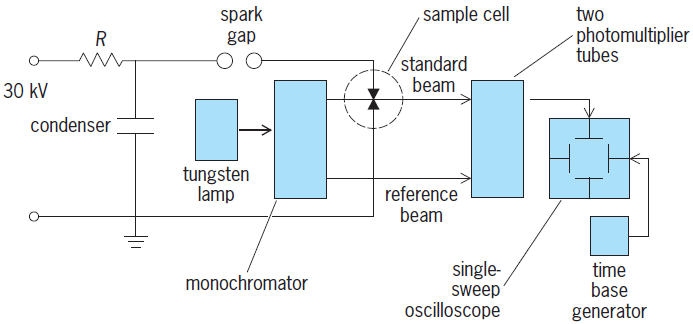
that kb ≃ 1.8 × 1011 dm3 mol−1 s−1. This is an exceptionally large rate constant for a bimolecular reaction between oppositely charged ions in aqueous solution and is, in fact, larger than that for any other diffusive encounter between ions in water. Eigen and L. DeMaeyer, who first determined this rate constant (using another relaxation method called the electric-field jump method), attributed the great speed of the back reaction of the equilibrium, reaction (5), to the exceptionally rapid motion of a proton through water, accomplished by the successive rotations of a long string of neighboring water molecules (Grotthuss mechanism). Since sample solutions can be heated by a mode-locked laser on a picosecond time scale or by a Bunsen burner on a time scale of minutes, the temperature jump (T-jump) relaxation method just described is very versatile. The choice of the particular means of effecting the temperature perturbation is dictated only by the requirement that the temperature rise somewhat more rapidly than the time constant of the chemical reaction to be explored, so that a tedious deconvolution can be avoided. The discharge of a high-voltage (15–30-kV) capacitor through the sample liquid containing sufficient inert electrolytes to make it a good electrical conductor is the now classic Joule heating T-jump method used by Eigen and coworkers in their pioneering studies. A schematic of such an apparatus is shown in Fig. 2. The 30-kV voltage generator charges the 0.1-microfarad condenser to the voltage at which the spark gap breaks down. The condenser then discharges across the spark gap and through the sample cell, containing an aqueous 0.1 M ionic strength solution, to ground. The sample cell is an approximately 50 ml (3.05 in.3) Plexiglas cell containing two platinum electrodes spaced 1 cm (0.4 in.) apart and immersed in an aqueous 0.1 M ionic strength solution. The surge of current raises the temperature of the 1-ml (0.061-in.3) volume of solution between the electrodes by 10°C (18°F) in a few microseconds.
Electric-field jump
In a situation, such as reaction (8), in which electrically neutral reactant species dissociate into oppositely charged ions, an especially sensitive tool for measuring rate constants of forward and backward reactions is the electric-field jump (E-jump) technique with conductometric detection. In a strong electric field (of the order of 4 × 106 V m−1), a weak acid in solution is caused to dissociate to a greater degree than it would in the absence of the electric field. For weak electrolytes, such as aqueous acetic acid or ammonia, the effect is the order of 10% or less of the total normal dissociation, even at very high electric-field strengths. However, with a sensitive, high-voltage, Wheatstone bridge, the exponential increase with time in the concentration of ions following a precipitous increase in electric-field strength is readily detected. The measured relaxation time (τ) is clearly that corresponding to the high-electric-field environment, but since the rate constants for these reactions differ little in and out of the electric field, no serious problem is posed.
A more serious concern is that the sample solution may have a very high electrical resistance, so that the supposedly square step function in the electric-field strength is distorted by a significant voltage drop with concomitant heating of the sample liquid. Problems of working with high voltages, balancing capacitive and inductive effects in a very sensitive conductance bridge (now often circumvented by spectrophotometric detection), and the comparative difficulty of evaluating amplitudes of relaxations (as opposed to their readily determined time constants) are all factors that have worked against the wide use of the E-jump technique. There are many more ways of achieving a T-jump than an E-jump, and ΔH° values for chemical equilibria are readily available in the thermodynamic literature, whereas the extent to which a chemical equilibrium is displaced by an electric-field increment is rarely already known and is difficult to determine. Thus the commercialization of the T-jump method and the comparative neglect of the E-jump relaxation technique are readily understood.
Notwithstanding these difficulties, the E-jump technique is without peer for the investigation of the kinetics of solvent autoionization or for the exploration of the properties of weak electrolyte solutes in exotic solvents such as acetonitrile or xenon (the latter liquefied under a pressure of about 50 atm or 5 megapascals), so long as the relaxation time to be measured lies in the range 30 nanoseconds < τ < 100 μs.
Ultrasonic absorption
Two other relaxation methods more widely used than the E-jump technique are pressure jump (P-jump) and ultrasonic absorption. Each relies for its effectiveness on a volume change, ΔV°, occurring in an aqueous sample equilibrium undergoing kinetic investigation. (In a non-aqueous solvent it will frequently be more important that ΔH° be large than that ΔV° be so for the equilibrium to be susceptible to study by these two relaxation techniques.) As electrically neutral, weak electrolyte solute species dissociate into ions in aqueous solution, there is an increase in the number of solvent molecules drawn into a highly ordered solvation sheath. The higher the charge density of the ion, the more water molecule dipoles are bound and the greater the change in V° as reactants become products. Thus the dissociation of an aqueous neodymium(III) sulfate complex is particularly susceptible to study by one or more of the four or five ultrasonic absorption methods that cover the f ≃ 100 kHz–1 GHz sound frequency range. Unlike the T-jump and E-jump relaxation methods, which usually employ step function perturbations, the ultrasonic absorption techniques are continuous-wave experiments in which the sample chemical equilibrium absorbs a measurable amount of the sound wave's energy when the frequency of the sound wave ( f ) and the relaxation time of the chemical equilibrium bear the relation to one another given by Eq. (10).
A particularly easy ultrasonic absorption experiment to understand and perform is the laser Debye-Sears technique. A continuously variable frequency sound wave is introduced by a quartz piezoelectric transducer into a 30-ml (1.83-in.3) sample cell that has entrance and exit windows for a visible laser light beam that passes through the cell at about 90° to the direction of travel of the planar sound wave. The regions of compression and rarefaction in the sound wave act as a diffraction grating for the laser light beam. If a chemical equilibrium in the sample strongly absorbs a particular frequency of sound ( f ), the definition of the “diffraction grating” will deteriorate and the measured intensity of the first-order diffracted laser light will diminish. The frequency of minimum diffracted light intensity will be that of Eq. (10). Figure 3 shows a diagram of the apparatus. The piezoelectric (quartz) transducer is cemented to the bottom of a plastic rod that is driven up and down by a computer-controlled stepping motor. The angle of diffraction of the laser beam by the alternating regions of compression and rarefaction in the liquid (suggested by the horizontal lines) is exaggerated in the diagram.
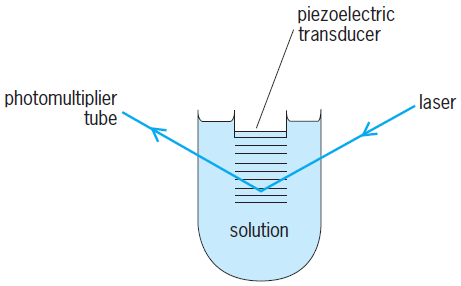
Ultrasonic absorption techniques have been used in kinetic investigations of complicated biophysical systems such as the order-disorder transitions that occur in liquid crystalline phospholipid membranes. While the ultrasonic techniques look through a conveniently broad time window at kinetic processes in solution, this picture window is difficult to “see through” in that many equilibrium processes in solution can absorb sound energy and the responsible process is not instantly identified by a characteristic absorption of electromagnetic radiation as in a spectrophotometric T-jump or E-jump experiment. A further disadvantage arises from the great breadth of the ultrasonic absorption “peaks” in a plot of normalized sound absorption versus sound frequency. Unless multiple relaxation times in a chemical system are quite widely separated in time, they are difficult to resolve in an ultrasonic absorption spectrum. See also: Ultrasonics
Pressure jump
The typical pressure-jump (P-jump) experiment is one in which a liquid sample under about 200 atm (20 MPa) pressure is suddenly brought to atmospheric pressure by the bursting of a metal membrane in the sample cell autoclave. Relaxation times measured spectrophotometrically or conductometrically are thus accessible if τ > 100 μs. This technique has proven particularly useful in the elucidation of micellar systems of great interest for catalysis and for petroleum recovery from apparently depleted oil fields.
The continuous- and stopped-flow techniques antedate somewhat the relaxation techniques described above, and have the sometimes important advantage of permitting kinetic measurements in chemical systems far from equilibrium. The stopped-flow experiment is one in which two different liquids in separate syringes are mixed rapidly in a tangential jet mixing chamber and then the rapid flow of mixed reactants is almost immediately brought to a halt in a spectrophotometric, conductometric, or calorimetric observation chamber. Reaction half-lives exceeding 2 ms are easily accessible. See also: Shock tube
Other relaxation methods
Stopped-flow equipment has been used in concentration-jump and solvent-jump relaxation kinetic studies. An example of an application of the solvent-jump technique to a system insensitive to concentration-jump is a kinetic study of reaction (11)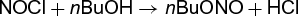 (11)
(11)
in mixed CCl4-acetic acid solvents of varying composition (Bu = butyl). The thermodynamic treatment of the solvent jump is just about the only aspect of the presently known relaxation techniques that was not described in exhaustive detail by the earliest publications of Eigen and DeMaeyer. See also: Chemical thermodynamics
Gas-phase reactions
The rates of thermal gas-phase chemical reactions are important in understanding processes such as combustion and atmospheric chemistry.
Elementary reactions, mechanisms, and rates
Chemical conversion of one stable, gas-phase molecule into another is an apparently simple process; yet it is highly unlikely to occur in just a single step, but as a web of sequential and parallel reactions involving many species. The oxidation of methane (CH4) to carbon dioxide (CO2) and water provides an excellent example. It occurs in combustion (for example, in burning natural gas, which is mostly methane) as well as in the atmosphere. In both cases, the net process may be written down as a single reaction (12).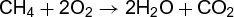 (12)
(12)
The reaction does not, however, result from collision of two oxygen (O2) molecules with one methane molecule. Rather, it involves many separate steps. A simplified list of the steps involved in reaction (12) for both combustion and for the atmosphere is given below.
Combustion: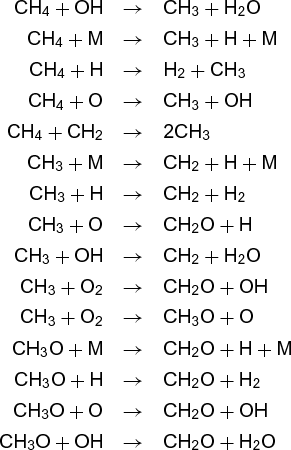
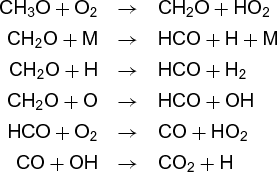
Atmospheric oxidation: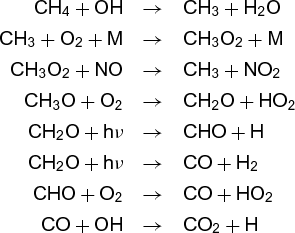
Even though the overall reaction is the same in both environments, the steps are quite different, as are the rates, temperature dependences, and by-products. Each is called an elementary reaction, and the sum of the steps that makes up the overall reaction is called the mechanism. Currently, the major thrust of chemical kinetics is to elucidate such mechanisms and to measure (or calculate) the rates of the elementary reactions.
All elementary reactions fundamentally require a collision between two molecules. Even in the case of a unimolecular reaction, in which a single molecule breaks apart or isomerizes to another form, the energy required for the process comes from collision with other molecules. The species involved in many gas-phase elementary reactions are free radicals, molecules that have one or more unpaired electrons. Such species tend to be highly reactive, and they are responsible for carrying out most gas-phase chemistry.
A reaction rate is the rate at which the concentration of one of the reactants or products changes with time. The objective of a kinetics experiment is not to measure the reaction rate itself but to measure the rate coefficient, an intrinsic property of the reaction that relates the reactant concentrations to their time rates of change. For example, the mathematical expression for the rate of a biomolecular reaction, A + B → products, is differential equation (13).
The square brackets denote the concentrations of A and B, and k is the rate coefficient described above. The dependence of the rate expression on reactant concentrations is determined experimentally, and it also arises from a fundamental tenet of chemistry known as the law of mass action. Once the rate constant is known, the rate of a reaction can be computed for any given set of concentrations.
Rate constants usually change with temperature because of the change in the mean energy of colliding molecules. The temperature dependence often follows an Arrhenius expression, k = A exp(−EA / RT), where A is a preexponential factor that is related to the gas-phase collision rate, R is the universal gas constant, and T is the absolute temperature (in kelvins). The key quantity is the activation energy, EA , the amount of energy required to induce a reaction. Pressure dependences are usually important only for association reactions, A + B → AB, since collision of A with B will form an energized complex, AB*, that will simply redissociate unless a subsequent collision carries away enough energy to stabilize the AB product. The probability of a stabilizing collision increases with the collision frequency and thus the total pressure.
In the simple case of a unimolecular reaction, A → P, the rate expression is Eq. (14).
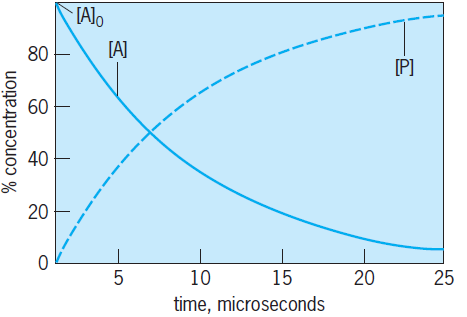
Equation (14) is first-order since the rate is proportional to the reactant concentration to the first power, and it leads to an expression for the change in the concentration of A or P with time (called an integrated rate expression), as in Eqs. (15).
The subscripts denote the concentrations at zero time (initial concentration) and an arbitrary time t. The concentration of A decreases (because it is reacting away) as a function of time, while the concentration of P increases with time such that the sum of the concentrations of A and P is always constant and equal to the initial concentration of A (Fig. 4). Because first-order reactions are mathematically simple, kineticists try to reduce all studied reactions (if at all possible) to this form. A second-order reaction, for example A + B → products, has the rate expression given in Eq. (13). To reduce the second-order expression to the first-order expression, Eq. (14), one chooses one of the concentrations to be in large excess, for example [B] ≫ [A]. The concentration of B is then approximately constant during the course of the reaction, and it may be combined with the rate constant to give an expression identical to Eq. (14) that depends on the concentration of A alone.
Experimental methods
The experimental challenges to rate constant measurements include generation of reactive species of interest, the measurement of their concentration on a time scale fast enough to follow the course of the reaction, and the measurement of the reaction time itself. The capability for measurement of small concentrations (down to a few molecules in a milliliter) and short times (down to femtoseconds; 1 fs = 10−15 s) has improved dramatically and has enabled kineticists to study extremely fast gas-phase reactions. The following examples illustrate how rate constants are measured.
The rate constant for the bimolecular reaction of OH with methane is very important. Figure 5a illustrates its measurement via the commonly used pulsed photolysis–laser induced fluorescence (PP–LIF) technique. A pulse of short-wavelength ultraviolet light from a laser irradiates a gas mixture containing a precursor molecule, such as hydrogen peroxide (H2O2) or nitric acid (HNO3), that absorbs the light and fragments instantaneously to produce OH. A second laser produces a pulse of light that is tuned to a color (wavelength) absorbed by the OH radicals, which in turn emit light (fluoresce) in all directions. The fluorescence intensity falling on a detector is proportional to the OH concentration. Both laser pulses have very short duration (typically <2 × 10−8 s or 20 nanoseconds) on the time scale of the reaction. The first pulse creates the OH radicals and defines zero time, and variation of the time delay between the two lasers varies the reaction time. Methane is present in large excess over OH, and thus its concentration, as measured by its pressure, is essentially constant during the course of the reaction. See also: Laser; Laser photochemistry
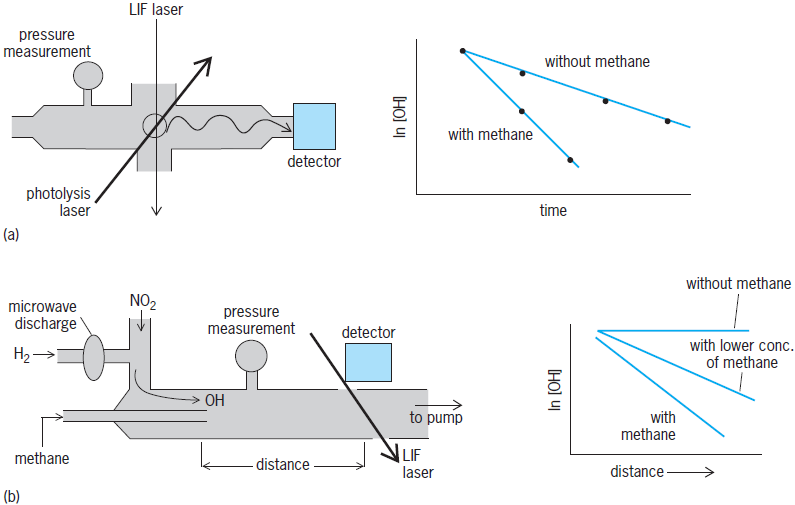
The same rate coefficient may also be measured using the apparatus shown in Fig. 5b. In this case, a flow of gas containing hydrogen (H2) passes through a microwave discharge, where H2 breaks down to H atoms. Then it reacts with nitrogen dioxide (NO2) to make OH and nitric oxide (NO). The NO is unreactive with methane and does not interfere with the OH reaction. Methane flows through a movable injector at the center of a flow tube. The two gas flows mix at the injector and initiate reaction between OH and methane. A laser-induced fluorescence detector, similar to the one described above, at the end of the tube measures the amount of OH present at that point. (Other detectors, such as a mass spectrometer, also can be used.) Since the gas flow velocity down the tube is constant, the distance from the injector to the mass spectrometer can be converted to a reaction time, and movement of the injector to different positions in the tube varies the reaction time. As above, its pressure in the flow tube gives the approximately constant methane concentration.
Both of the above examples are direct methods in which the time rate of concentration change is directly observed. Relative rate constant measurements can be done for the determination of the rate constant for reaction of OH with hydrofluorocarbon 134a (HFC-134a). This compound is used as an automobile refrigerant in place of the banned CFCs (chlorofluorocarbons), and, similar to methane, its reaction with OH determines its degradation rate in the atmosphere. The OH radicals are continuously produced in a mixture containing both methane and HFC-134a, and the depletion of methane and HFC-134a is measured. The ratio of the depletions is then proportional to the rate constants for reaction of OH with each compound. Since the rate constant for reaction of OH with methane is known, the measurement provides the previously unknown rate constant for reaction of OH with HFC-134a.
There are many other techniques for measurement of reactant or product concentrations, including ultraviolet, visible, and infrared light absorption, gas chromatography, and a host of additional fluorescence and mass spectrometric methods.
Complex gas-phase chemical reactions may be broken down into elementary steps that describe reactions at the level of collisions between individual molecules. The rate constants for such elementary steps allow calculation of the reaction rates from reactant concentrations as well as kinetic modeling of larger chemical processes. Determination of elementary rate constants involves measurement of reactant or product concentrations on the time scale of the reaction. Rate constants may also be made in a relative fashion in cases where two reactions share a common reactant and one rate constant is known.





