Key Concepts
The transfer of thermal energy by actual physical movement from one location to another of a substance in which thermal energy is stored. Heat convection is often the primary mode of energy transfer in liquids and gases. A familiar example of convection is the boiling of water in a pot (Fig. 1). Technically, convection denotes the nonradiant heat exchange between a surface and a fluid flowing over it. (The term "fluid" refers to deformable forms of matter, including liquids, gases, and plasmas.) Although heat flow by conduction also occurs in this process, the controlling feature is the energy transfer by flow of the fluid—hence the name convection. Convection is one of the three basic methods of heat transfer, the other two being conduction and radiation. See also: Gas; Fluids; Heat; Heat conduction; Heat radiation; Heat transfer; Liquid; Plasma (physics)

Types of heat convection
The two types of heat convection are natural (free) convection and forced convection. The two types are often co-present in real-life heat transfer situations, known as mixed convection. A familiar example is the free or forced movement of warm air throughout a room to provide heating. See also: Comfort heating; Heating system
Natural convection
This mode of energy transfer is exemplified by the cooling of a vertical surface in a large quiescent body of air at temperature t∞. The lower-density air next to a hot vertical surface moves upward because of the buoyant force of the higher-density cool air farther away from the surface (Fig. 2a). At any arbitrary vertical location x, the velocity parallel to the surface will increase from zero at the surface to a maximum, and then decrease to zero as ambient surrounding conditions are reached (Fig. 2b). In contrast, the temperature of the air decreases from the heated wall value to the surrounding air temperature. These temperature and velocity distributions are clearly interrelated, and the distances from the wall through which they exist are coincident because, when the temperature approaches that of the surrounding air, the density difference causing the upward flow approaches zero.
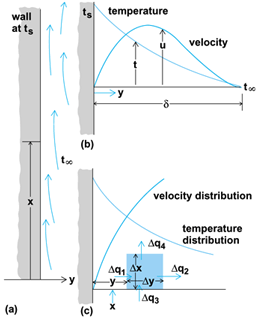
The region in which these velocity and temperature changes occur is called the boundary layer. Because velocity and temperature gradients both approach zero at the outer edge, there will be no heat flow out of the boundary layer by conduction or convection. See also: Boundary-layer flow
An accounting of all of the energy streams entering and leaving a small volume in the boundary layer (Fig. 2c) during steady-state conditions yields Eq. (1),
where κ, ρ, and cp are the thermal conductivity, the mass density, and specific heat at constant pressure of the air, and u and v are the velocity components in the x and y directions, respectively. Equation (1) states that the net energy conducted into the element equals the increase in energy of the fluid leaving (convected) over what it had entering.
Very close to the surface, the velocity components u and v both approach 0, and the partial derivatives ∂2 t/∂x2 and ∂t/∂x also approach 0. Therefore, the heat transfer from the wall must be by conduction through a thin layer of air which is effectively stationary relative to the surface. Thus, Eq. (2)
is obtained, where q is the time rate of heat flow per unit of surface area through an infinitesimally thin layer of air. At a very small distance from the surface, the velocity becomes finite and some of the energy conducted normal to the surface is convected parallel to it. This process causes the temperature gradient to decrease, eventually to zero. The solution of a problem requires simultaneous determination of the velocity and temperature distributions throughout the boundary layer. From this, the temperature gradient at the wall and the rate of heat flow can be computed.
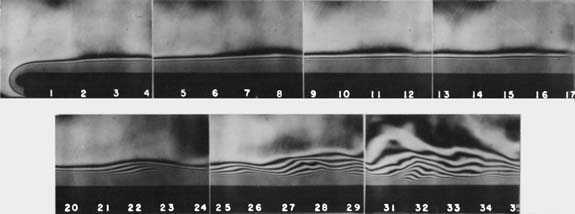
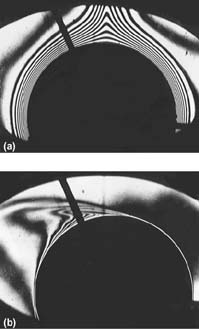
The effect of energy leaving a surface and remaining in the boundary layer is (1) a gradual increase in temperature of the air in this layer as it moves upward, and (2) diffusion of energy farther from the surface, entraining more air in (thickening) the boundary layer. This effect can be visualized with interference photographs (Figs. 3 and Fig. 4a), where the interference fringes indicate lines of constant temperature (isotherms).
Forced convection
If air is blown across a cylinder (Fig. 4), the boundary layer on the forward half of the cylinder will become so thin that it is not possible to resolve the isotherms within it. Although the natural convection forces are still present in this latter case, they are clearly negligible compared with the imposed forces. The process of energy transfer from the heated surface to the air is not, however, different from that described for natural convection. The major distinguishing feature is that the maximum fluid velocity is at the outer edge of the boundary layer. This difference in velocity profile and the higher velocities provide more fluid near the surface to carry along the heat conducted normal to the surface. Consequently, boundary layers are very thin.
The properties of a fluid which influence its heat-convecting ability are the dynamic viscosity μ, heat capacity at constant pressure cp, and thermal conductivity κ. These combine in a single significant property in the form μcp/κ = μ/(κ/cp), which is the ratio of the fluid viscosity to the quotient of its heat-conducting and heat-storage capacities. With proper units, this ratio is dimensionless and is called the Prandtl number, NPr . For air NPr is approximately 1. Fluids such as oils have values greater than 100. Liquid metals, for which NPr ∼ 0.01, are particularly effective for convective heat-transfer applications.
Heat-transfer coefficient
The convective heat-transfer coefficient h is a unit of conductance used for calculation of convective heat transfer. It was introduced by English physicist and mathematician Isaac Newton and, until the mechanism of convection was properly interpreted, was thought to be a characteristic of the fluid flowing. To describe quantitatively the cooling of objects in air, Newton suggested Eq. (3).
This equation, known as Newton's law of cooling, is really a definition of h. By comparison with Eq. (2), this coefficient can be seen to be proportional to the slope of the fluid temperature distribution right at the surface, and the thermal conductivity κ of the fluid. Metric units are W/(m2)(°C); common engineering units are Btu/(h)(ft2)(°F).
As the fluid in the heated or cooled boundary layer moves along an isothermal surface, it gradually approaches the temperature of the surface. This causes the temperature gradient in the fluid at the surface (and the rate of heat transfer) to decrease in the direction of flow. Taking, for example, an airstream at 104°F (40°C) moving at 50 ft/s (15 m/s) over a flat plate at 68°F (20°C), the local heat-transfer coefficient hx decreases in 1 ft (0.3 m) to about one-fifth of its leading-edge value. For practical calculations, an average heat-transfer coefficient h is more useful. It is obtained by integrating hx over the heat-transfer surface and dividing by the surface area. For this system, h is a function of the plate length l, κ, μ, ρ, and u∞ of the fluid. For comparing geometrically similar systems involving different fluids, dimensional analysis shows that the specific properties can be combined into dimensionless parameters, conveniently reducing the number of independent variables. For the flat plate, these are the Nusselt number, NNu = h l/κ, the Reynolds number, NRe = lu∞ρ/μ, and the Prandtl number, NPr . For example, it can be shown that in this case Eq. (4)
holds. In the case of free convection, the Grashof number, NGr = βgl3 Δt/ν2 (where β is the coefficient of thermal expansion, and ν = μ/ρ), replaces the Reynolds number. The product of NGr and NPr is known as the Rayleigh number (NRa ), and is used in correlating free convection transfer. Other dimensionless numbers pertinent to convection include the Stanton number, NSt = h/ρucp = NNu /NRe NPr , which is related to the skin-friction coefficient. See also: Dimensional analysis; Reynolds number
Turbulent flow
Heat convection in turbulent flow is interpreted similarly to that in laminar flow, which has been implied in the above discussion. Rates of heat transfer are higher for comparable velocities, however, because the fluctuating velocity components of the fluid in a turbulent flow stream provide a macroscopic exchange mechanism which greatly increases the transport of energy normal to the main flow direction. For example, if free-stream turbulence caused the boundary-layer flow in the example above to be turbulent, the heat-transfer rate would be about 2.5 times higher. Because of the complexity of this type of flow, most of the information regarding heat transfer has been obtained experimentally. Such results, combined with dimensional analysis, have yielded useful design equations, typical of which is Eq. (5),
for predicting the heat transfer in a pipe, where d is the pipe diameter.
An illustration of the controlling effect of fluid flow on convective heat transfer is provided by measurements of the local variation around a bluff body such as a cylinder normal to an airstream of velocity u∞. Major changes occur in the streamline pattern as u∞ is increased from very low to high values (Fig. 5). At very low velocities the flow at the edge of the boundary layer is slowed to zero as it approaches the forward stagnation point. It accelerates as it flows around the cylinder to a maximum at an angle from the stagnation point θ = 90°, and then decelerates to zero at the rear. As the free-stream velocity is increased, the flow separates from the surface before reaching θ = 180° (Fig. 5a). With further increase the separation point moves farther forward (Fig. 5b). When the Reynolds number, NRe =Du∞ρ/μ (where D is the cylinder diameter), reaches about 1 × 105 (Fig. 5c), the flow in the boundary layer around θ = 90° becomes turbulent. Thus, the boundary can remain attached to the surface longer and the separation point moves toward the rear (Fig. 5d). This change may be delayed until NRe reaches as high as 5 × 105 in a low-turbulence-level airstream.
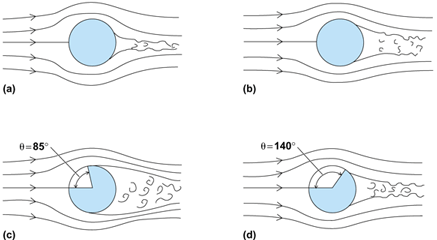
Dramatic changes in the local rate of heat transfer are produced by these changes in the flow. For NRe ≥ 140,000, the local heat transfer rises rapidly from a minimum around θ = 90° to a maximum and then decreases to a second minimum around 140°. This variation is due to the change to turbulent flow before separation on the rear of the cylinder occurs. See also: Laminar flow; Turbulent flow
Condensation and boiling
Condensation and boiling are important phase-change processes involving heat release or absorption. Because vapor and liquid movement are present, the energy transfer is basically by convection. Local and average heat-transfer coefficients are determined and used in the Newton cooling-law equation for calculating heat rates which include the effects of the latent heat of vaporization.
Condensation
Consider a saturated or superheated vapor of a single substance in some region. When it comes in contact with a surface maintained at a temperature lower than the saturation temperature, heat flow results from the vapor, releasing its latent heat and condensing on the surface. The condensation process may proceed in two more or less distinct ways. If there are no impurities in the vapor or on the surface (which need not be smooth), the condensate will form a continuous liquid film. If, however, such contaminants as fatty acids or mercaptans are present, the vapor will condense in small droplets. These droplets increase in size until their weight causes them to run down the surface. In doing so, they sweep the surface free for formation of new droplets. For the same temperature difference between the vapor and surface, heat transfer with dropwise condensation may be 15–20 times greater than filmwise condensation. The dropwise type is therefore very desirable, but conditions under which it will occur are not predictable, and designs are limited to systems for which experimental results are available. See also: Condensation; Lipid
Boiling
In boiling, results indicate the existence of several regimes. The important independent variable is the temperature difference Δt between the hot surface and the fluid relatively far from the surface. For values of Δt up to approximately 10°F (6°C), the liquid is being superheated by natural convection, and q/A is proportional to Δt. With further increase in Δt, bubbles form at active nuclei on the heated surface. These bubbles break away and rise through the pool, their stirring action causing the heat transfer to be much above that due to natural convection. This phenomenon is called nucleate boiling, and q/A varies as Δt3 to Δt4 . When the rate of bubble formation becomes so rapid that the bubbles cannot get away before they tend to merge, a vapor film begins to form, through which heat must flow by conduction. The rate of heating then decreases with Δt until complete film boiling is reached and heat flows by radiation and conduction through the film. See also: Boiling; Boiling point
The high heat rates which occur during boiling make it a very effective means of absorbing the energy capable of being released in furnaces and nuclear reactors. The high heat rates are also one reason why the vapor power-generating cycles have been successful. See also: Boiling processes





