Key Concepts
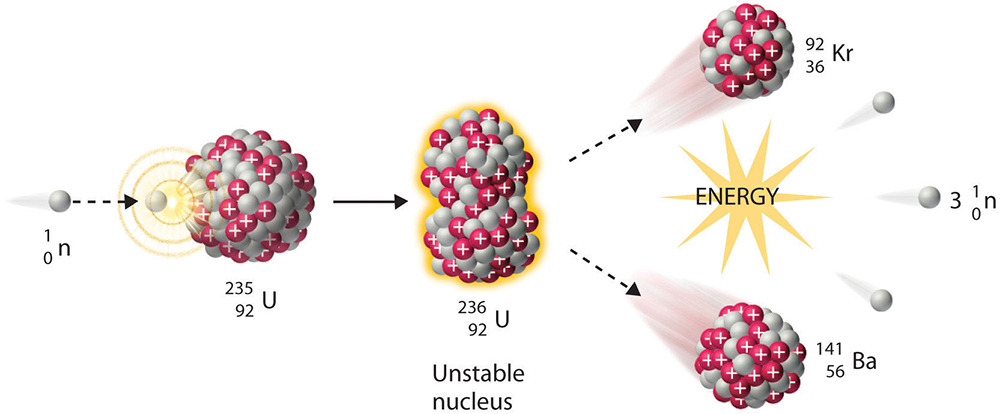
The extreme deformation of a very large nucleus followed by splitting of the nucleus into lighter nuclei, predominantly two lighter fragments, in conjunction with a large energy release. Fission is a naturally occurring spontaneous decay process of heavy isotopes and can also be induced by the absorption of particles, such as neutrons, protons, or photons, under appropriate conditions (Fig. 1). More broadly, fission results from disruption of the delicate balance between the attractive nuclear force and the repulsive Coulomb force within a large nucleus and is driven by the fact that nuclear binding energy is maximized for medium-mass nuclei. The development of nuclear physics and the fission process during the twentieth century has played an important role in the technical sector, for instance, with regard to electricity production and medical therapies, as well as affected cultural development and political decision making. See also: Atomic nucleus; Coulomb excitation; Energy; Isotope; Nuclear physics; Photon
Brief history
The discovery of fission, experimentally in late 1938 and theoretically explained in early 1939, represented a culmination of decades of work in the developing fields of radioactivity and nuclear physics. A key event occurred in 1934, when Italian-born U.S. physicist Enrico Fermi claimed that neutron capture by an isotope could lead eventually to a residual nucleus of atomic number, Z, one unit higher than the isotope, thus leading to new radioactive elements. German radiochemist Otto Hahn, Austrian-born Swedish physicist Lise Meitner (Fig. 2), and German chemist Fritz Strassmann subsequently applied this novel neutron irradiation technique to create transuranic elements—elements with an atomic number beyond uranium (Z = 92), the heaviest naturally occurring element. See also: Atomic number; Neutron; Uranium

Although this undertaking eventually proved successful, it initially yielded confusing chemical results by seemingly also producing a lighter element, barium (Z = 56), in very high yields. Through meticulous radiochemical techniques, Hahn and Strassmann confirmed in 1939 that barium was indeed present among the products, along with many other intermediate-mass nuclei, following the bombardment of uranium by neutrons. Their work further revealed that the energy released in the bombardment was orders of magnitude greater than any previously known decay. Ida Noddack, another German chemist who had worked with Fermi, had earlier proposed that lighter elements could be formed by this type of bombardment. However, it was Meitner and Austrian-born British physicist Otto Frisch, now supported by the undisputed results of Hahn and Strassmann, who provided the correct understanding of the counterintuitive experimental findings in 1939. They explained that the uranium nuclei following neutron capture are highly unstable and split in a process that Frisch coined as “fission,” in analogy to the biological process of cell division. For example, one of many possible fission reactions these scientists may have explored is written as:
Nuclear binding energy
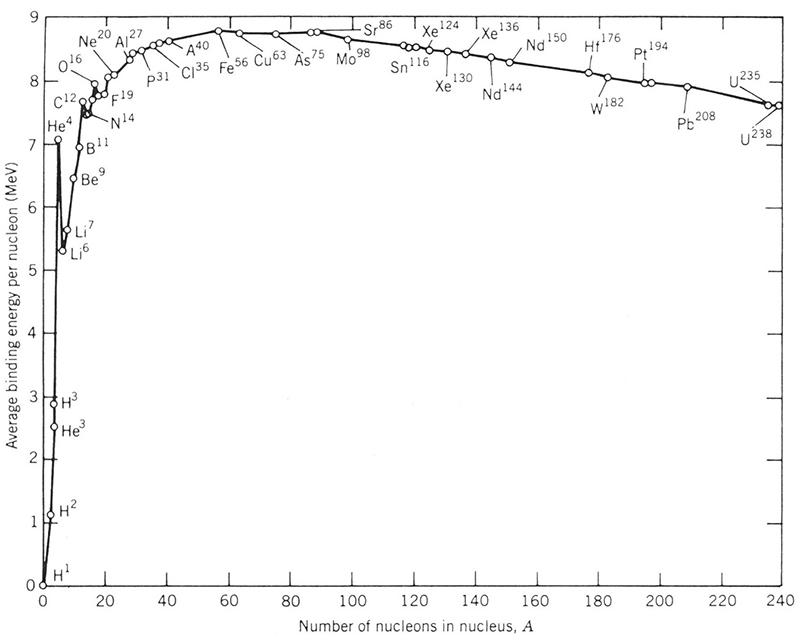
When an ensemble of free nucleons (protons and neutrons) come together, the nucleus that is formed has less mass than the sum of the masses of the individual free nucleons. This mass difference is emitted in the form of energy and is called the binding energy of that nucleus. The binding energy that is released during the formation of a nucleus is what would have to be supplied to decompose the nucleus back into its individual components. The average binding energy is approximately 8 MeV per added nucleon for stable nuclei, and decreases slowly for exotic isotopes of a given element. Careful examination of the variation of the binding energy per nucleon (BE/A) with total mass, as in the curve shown in Fig. 3, has the interesting behavior of a rapid increase followed by a slow decline. A larger binding energy per nucleon implies a more tightly bound and thus a more stable nucleus. The peak in stability, as seen in Fig. 3, can be seen to occur around mass A = 56. Consequently, it is possible that a nucleus of greater mass (A > 56) could find it energetically favorable to convert to a more stable system by breaking into lighter fragments nearer to this peak. The small binding energies of the lightest nuclei do not favor breaking into many small pieces. The transformation of a very heavy nucleus into two major fragments is the fission process, and the difference in binding energy (or, equivalently, mass) between the initial nucleus and the final system provides fission’s large energy release. See also: Mass; Nuclear binding energy; Nucleon
Liquid-drop model
The earliest description of a nucleus that could successfully characterize the binding energy curve of Fig. 3 was the so-called charged liquid-drop model. By the mid-1930s, a variety of experiments had demonstrated that nuclei are generally spherical and incompressible, reminiscent of a liquid droplet, and the nucleons could be viewed analogously to molecules. This phenomenological treatment of the collective behavior of the overall nucleus was first developed by Russian-born U.S. physicist George Gamow, German physicist Werner Heisenberg, and German theoretical physicist Carl Friedrich von Weizsäcker.
The fundamental liquid-drop model provides a parametric equation for the binding energy that contains the following five terms:
- Volume term: Each nucleon feels the same attraction from its nearest neighbors due to the strong force. This term provides the overall stability of the nucleus.
- Surface term: A correction to the volume term resulting from the finite size of the nucleus. Some nucleons must reside on or near the nuclear surface and therefore have fewer nearest neighbors than nucleons in the interior and so are less tightly bound. This term is then proportional to the nuclear surface area and reduces overall binding energy. This effect creates the surface tension along the “skin” of a droplet.
- Coulomb term: A repulsive term that tends to disrupt the nucleus and thus reduces the overall binding energy. The nucleus contains protons in close proximity to one another, each of which has an electrostatic repulsion for every other proton in the nucleus.
- Symmetry term: A quantum mechanical correction term arising in part from the Pauli exclusion principle. Protons and neutrons are distinguishable particle types and as a result can exist in the same quantum states. It is always energetically favorable for a nucleus to fill the lowest quantum states first, and thus equal numbers of protons, Z, and neutrons, N, would reside in the same states and be in close proximity, which enhances the nuclear attractive force. The greater the asymmetry between proton and neutron numbers, the more this term reduces binding energy. See also: Exclusion principle
- Pairing term: A final quantum correction due to the intrinsic angular momentum (spin) of the nucleons to account for the fact that paired nucleons (with opposite spins) are more bound than unpaired nucleons. This term depends separately on the numbers of protons and neutrons and thus can add to, have no effect on, or detract from the overall nuclear binding energy, depending on whether Z and N are both even, either Z or N is odd, or both Z and N are odd, respectively.
Ultimately, the liquid-drop model remains an approximation yet very successfully predicts the general trends of nuclear binding energy.
Meitner and Frisch applied this liquid-drop interpretation to explain their fission discovery in 1939. Specifically, they predicted that an external perturbation, such as the absorption of an incident neutron, can create surface waves that lead to a change in the shape of a liquid drop or nucleus. After the delicate energy balance of the round liquid drop is disturbed, the Coulomb force among the protons can cause an elongation of the drop. If the produced deformation is sufficiently large, the Coulomb repulsion among the elongated portions of the drop can produce a two-lobe structure and push the lobes farther apart until surface tension is totally overcome. The Coulomb force can then drive the system to the scission point, where the necking of the structure disappears, causing a complete split, or fission, of the initial nuclear drop into two droplets. A visualization of this description is shown in Fig. 4.
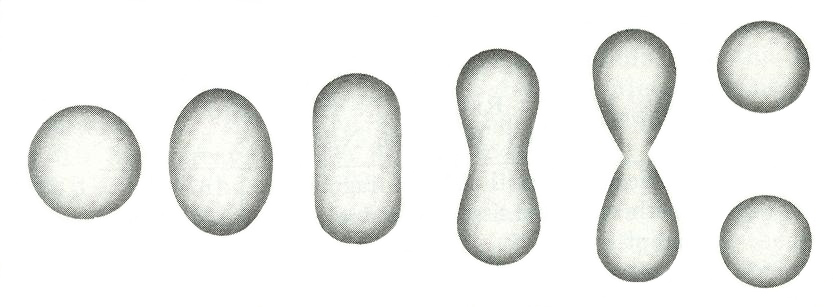
Later in the same year, Danish physicist Niels Bohr and U.S. theoretical physicist John Archibald Wheeler performed the first extensive calculations on nuclear fission using this model and demonstrated quantitatively the important competition in the splitting process between the nucleus’s repulsive electrostatic Coulomb force and its attractive surface tension. Detailed quantum mechanical and statistical models have been developed since to continue the study and description of the complex fission process. Nuclear fission remains an active area of research to this day because of the complexity of the process and the interplay of quantum mechanics and macroscopic forces, with work still to be done by experimentalists, theorists, and computational scientists. See also: Quantum mechanics
Characteristics of fission
Fragment mass distribution
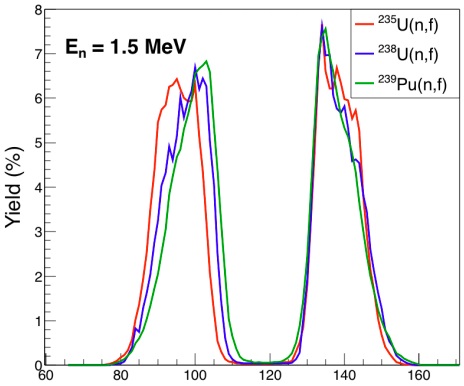
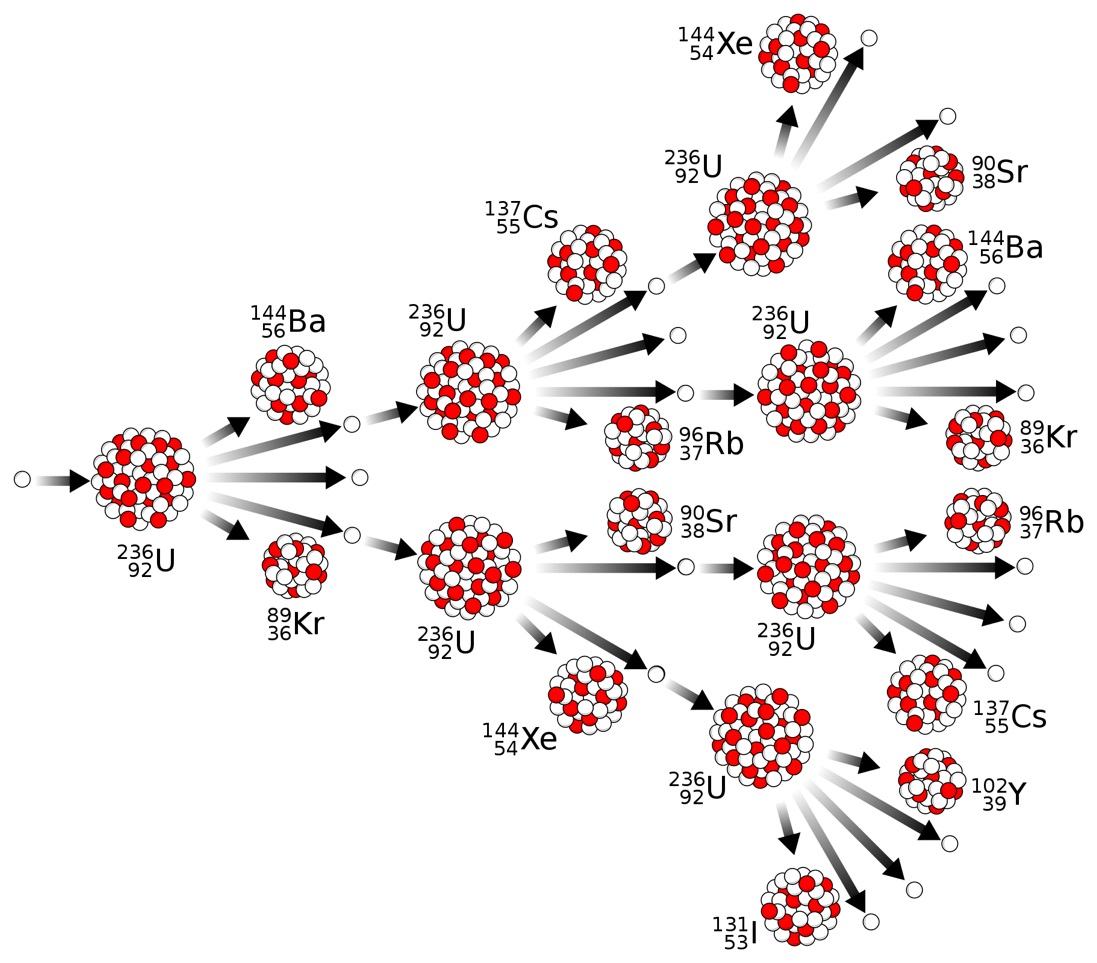
Every fission event can be different, and the fission fragments from the splitting process are not determined uniquely but rather follow a random statistical path. That is, every nuclide/isomer (product) has a certain probability, termed its independent fission yield, that it will be produced by fission, usually given as a percentage. This independent yield also depends on the parent nucleus that fissions as well as on the type of perturbation (thermal neutron absorption, fast neutron absorption, etc.) that leads to fission. As an example, three independent fission yield distributions are shown as a function of mass, A, for neutron-induced fission in Fig. 5. The overall distributions are doubly peaked, emphasizing that fission generally produces two fission fragments. It can additionally be noted that fission into equal or nearly equal fragments (A1 ≃ A2) is highly improbable in these cases and instead there is generally a light fragment (A1 ∼ 100) produced with a heavy fragment (A2 ∼ 132). The exact locations of the high-mass peaks correspond to isotopes with high binding energies predicted from quantum shell effects and remain fixed, though the complex path to fission gives a variety of fragments. The production of equal-mass fragments from actinide targets becomes more likely only as the fission-inducing particles become very energetic.
Ternary fission (three fragments) is possible but rare (∼ 0.4% probability per fission) and quaternary fission is even more rare.
Neutron emission
Conservation of protons and neutrons is necessarily maintained throughout the fission process, thereby leading to fission fragments (that is, nuclei) that are extremely rich in neutrons. The fission fragments shed this neutron excess through the emission of one or more neutrons at the instant of fission, within 10−16 seconds of a perturbation event. As a point of reference, the nucleus splitting occurs in approximately 10−20 seconds after a perturbation event. These rapidly shed neutrons are known as prompt neutrons, and the number of them emitted in each fission event is termed the neutron multiplicity. Neutron multiplicity follows an approximately Poisson distribution for each fissioning nucleus, but its magnitude is a function of the specific resultant fragments. Experimentally observed values for average neutron multiplicity include 2.48 for 233U, 2.42 for 235U, and 2.86 for 239Pu.
In addition to the prompt neutrons, delayed neutron emission is another possibility following a fission event. Delayed neutrons can be emitted after a fission fragment experiences beta decay. In comparison with prompt neutrons, delayed neutron emission occurs on a much longer timescale, on the order of seconds. The total intensity of delayed neutrons is near 1 per 100 fissions. See also: Beta-delayed neutron emission
The nuclei that are produced from fission fragments following prompt neutron emission are distinguished as fission products. When neutron emission ceases, gamma-ray emission may still occur to further de-excite the fission product and beta decay will occur as needed in order to drive the system to stability. See also: Gamma ray
Energy of fission
The energy released in fission events, calculated from the mass difference between the initial system and the products according to the mass-energy equivalence principle, is around 180–190 megaelectronvolts (MeV). An additional 10–20 MeV is released from neutron and gamma emission thereby giving the rule of thumb that a typical fission event releases approximately 200 MeV. For reference, a fission reaction produces around one million times more energy per unit mass than chemical reactions. See also: Electronvolt
The majority of the fission energy, around 80%, is carried away as kinetic energy and excitation energy of the fission fragments. However, fission fragment energies are also not unique, and in a fission event (even one that produces the same mass fragments), the resulting fragment energies may not be equivalent. Improving the predictions of fission yields, kinetic energies, excitation energies, timing, fragment electrical charge, and more is central to ongoing fission modeling efforts.
Fission cross sections
The heaviest nuclei have positive binding energies and thus there is an activation energy or “fission barrier” associated with initiating the fission process. A nucleus can undergo fission spontaneously when its excitation energy is greater than that of the fission barrier. This barrier can be thought of as a quantum mechanical potential, as indicated in Fig. 6 for one dimension, arising as a result of the competing effects of surface tension and electrostatic repulsion. Quantitative characterization of the fission barrier, however, is an extremely complex subject and is not well represented by the basic phenomenological liquid-drop model. An added complexity is that quantum mechanics allows “tunneling” through barriers even when the excitation energy is less than the barrier energy. The tunneling probability increases exponentially as the energy gets close to the top of the barrier, and some of the heaviest nuclei undergo spontaneous fission without any external perturbation. See also: Tunneling in solids
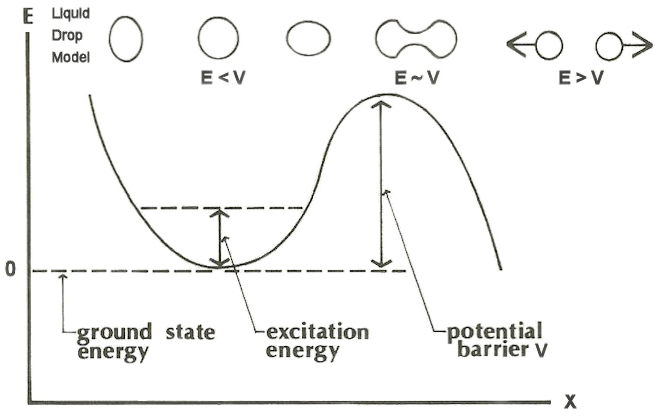
Nuclei can be classified by whether or not they will have excitation energy sufficient to fission after absorbing a zero-energy incident neutron:
- Fissile nuclei, such as 235U, can absorb a neutron of zero kinetic energy and reach an excitation energy already over the fission barrier.
- Fissionable nuclei, such as 238U, have a threshold to fission and require that the incident neutron bring in additional kinetic energy to overcome the fission barrier.
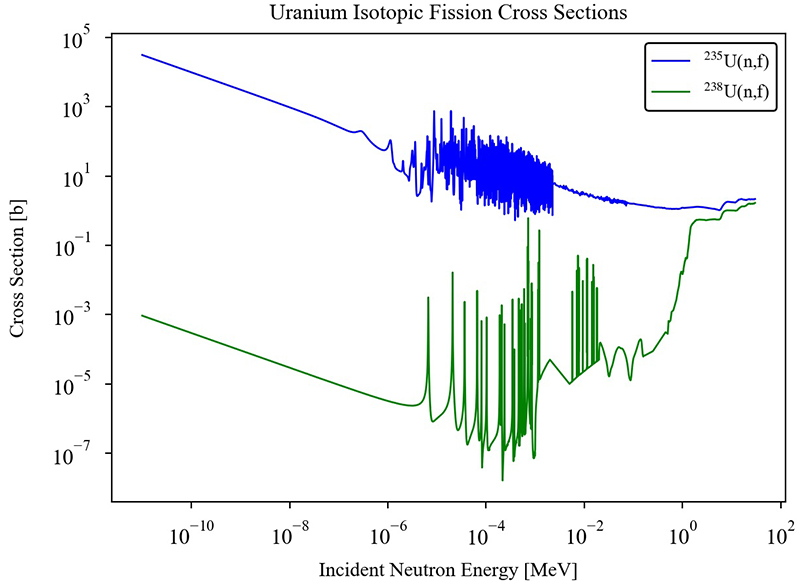
This fissile versus fissionable property broadly results in two different magnitudes of the fission cross section (akin to probability for reaction), as seen in Fig. 7, which shows neutron-induced fission of 235U and 238U. Notably, the shapes of the two curves are somewhat similar, and both increase at low energies that are inversely proportional to neutron velocity. 235U has a very high fission probability in the thermal region. 238U has a very low fission probability in the thermal region, and only past a certain threshold, at higher neutron energies, do the fission probabilities between the two uranium isotopes become similar. Accordingly, the pairing term in the liquid-drop model is central in accounting for fissile or fissionable behavior of nuclei. In this case, neutron capture in 235U produces an even–even nucleus and more excitation energy than neutron capture by 238U, which produces an even–odd nucleus.
Applications of fission
Each neutron emitted as a result of a fission event is capable of producing another fission event if it is captured in a neighboring heavy nucleus, which itself could yield more neutrons that could lead to more fissions, and so on. This process is known as a chain reaction. The condition for a chain reaction is usually expressed in terms of the neutron multiplication factor, k, defined as:
When k = 1, each fission event goes on to create one other fission event on average and the chain reaction continues and is called critical. A critical chain reaction is in a steady state. This is in contrast to when k < 1, called subcritical, when the fissioning of the material cannot continue indefinitely and eventually the reaction stops. A steady state is also not achieved when k > 1, a condition called supercritical, when more and more neutrons are produced at every stage of fission, causing an unstable, runaway chain reaction. This concept of supercriticality is illustrated in Fig. 8. See also: Chain reaction (physics)
Maintaining a critical fission environment given the proper fuel, geometry, coolant, neutron absorbers, and material parameters allows a sustained and steady release of energy, which is the basis for power-generating fission reactors. In brief, power reactors are devices for extracting the kinetic energy of fission fragments as heat and converting the heat energy to electrical energy, generally by boiling water and driving a turbine with the resulting steam. It is important to note that the delayed neutron emissions, though small in intensity, are essential for the control of nuclear reactors. No mechanical system could respond rapidly enough to prevent statistical variations in the prompt neutrons from causing the reactor to run out of control, but it is indeed possible to achieve mechanical control using the delayed neutrons. See also: Nuclear power
Fermi led a team that created the world’s first artificial sustained nuclear chain reaction with the so-called Chicago Pile-1 nuclear reactor in 1942. Natural nuclear reactors have also formed on occasion, such as at the Oklo Uranium Mine in Gabon, Africa, where it was discovered that nearly 2 billion years ago, sustained fission reactions took place over the course of 300,000 years. See also: Nuclear reactor
Fission reactors are also essential for production of medical isotopes. Large quantities of therapeutic and diagnostic isotopes, such as 99Mo/99mTc, can be retrieved from the fission products from reactors and are used globally in clinics and hospitals. See also: Nuclear medicine; Radiology
Supercriticality, and the associated exponential increase in energy release, is the basis of atomic (fission) bombs and two-stage thermonuclear (hydrogen) bombs. The materials, geometry, timing, fuel properties, and controls of these weapon systems are inherently different from those in commercial fission reactors. See also: Atomic bomb; Hydrogen bomb; Nuclear explosion; Thermonuclear reaction
Fission additionally plays a role in stellar nucleosynthesis to terminate the rapid neutron capture process (r-process). See also: Nucleosynthesis





