Key Concepts
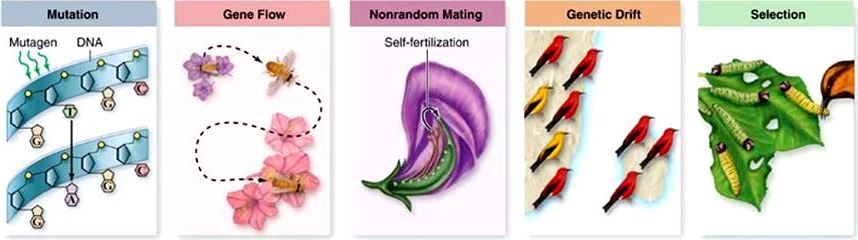
The study of both experimental and theoretical consequences of Mendelian heredity on the population level. Population genetics is the study of genetic variation within populations and is concerned with the kinds of alternate gene forms (alleles) within a population. In general, the field of population genetics stands in contradistinction to classical genetics (which deals with the offspring of specified parents on the familial level). Population genetics investigates the frequencies of genes, genotypes, and phenotypes, as well as the type of mating systems. It also studies the forces that may alter the genetic composition of a population in time (such as recurrent mutation, migration, and intermixture between groups), selection resulting from genotypic differential fertility, and the random changes incurred by the sampling process in reproduction from generation to generation (Fig. 1). The study of population genetics contributes to an understanding of the elementary step in biological evolution. See also: Allele; Biometrics; Evolution; Gene; Genetics; Human genetics; Mendelism
Mendelian populations
A Mendelian population is the unit of study in population genetics. Specifically, a Mendelian population is a group of individuals who interbreed among themselves according to a certain system of mating and form a breeding community. These individuals share a common gene pool that is the total genic content of the group. The population may be very large or very small, and is distinguished from species or varieties, which may consist of numerous isolated or partially isolated Mendelian populations. Mendelian population is a genetic rather than a taxonomic term. Mendelian populations differ from each other in their genic content or chromosomal organization; they do not necessarily differ in their taxonomic features. The term deme, originally defined as an assemblage of taxonomically closely related individuals, has been used as a synonym for Mendelian population. However, gamodeme, that is, a deme forming an isolated local intrabreeding community, would be a better substitute. See also: Population ecology
Mutation pressure
Gene mutation arises from time to time in nature. The causes for mutation are not fully known; thus, it can be said that mutations arise "spontaneously." The effect of a new mutant gene is unpredictable, and the gene is therefore said to mutate "at random." One property of mutation has been established; that is, it is recurrent. Each type of gene mutates at a certain rate per generation. The rate is usually low—about 1 mutant in 105–108 genes of a given sort, varying from locus to locus on the chromosomes, even under uniform conditions. Ionizing radiation, various chemicals, heat, and certain other agents increase the rate of mutation. See also: Mutation
Let μ be the rate of mutation from an allele A to another form a per generation. If a fraction p of the genes of a population is A in one generation, then the frequency of A in the next generation will be diminished by the amount pμ, so the new frequency of A will be p(1 − μ). The amount of change, pμ, is said to be due to the mutation pressure. If this pressure is unopposed generation after generation, the gene A will gradually disappear from the population. Therefore, for all existing genes, there must be some kind of compensating mechanism that supports its continuing presence in nature. One important problem in population genetics is the mechanism of maintenance of a gene in a population or its change in frequency from generation to generation.
In addition to the mutation from A to a, there can be a reverse mutation from a to A. If the opposing mutation alterations cancel each other, there will be no change in gene frequency, despite the recurrent mutations. This state of affairs is said to be in equilibrium.
In nature, and under artificial conditions, the mutation rates may not remain constant in all generations, but may fluctuate within a certain range from time to time. In such cases, instead of a single fixed equilibrium point, there will be an equilibrium distribution within a certain range, and the apparent change in gene frequency from one generation to the next may be purely a stochastic phenomenon without necessarily having long-term significance. See also: Stochastic process
Migration and intermixture
If a fraction m of a population with a gene frequency q consists of immigrants from outside, and the immigrant group has a gene frequency q(imm), the new gene frequency of the population will be q1 = (1 − m)q + mq(imm) = q − m[q − q(imm)]. Thus, the amount of change in gene frequency in one generation is Δq = q1 − q = −m[q − q(imm)]. This expression for Δq is of the same form as that for mutation. If the immigrants have the same gene frequency as the population, there will be no change in gene frequency, in spite of the migrations. The continued intermixture of neighboring populations will eventually make them homogeneous in terms of gene frequencies. Therefore, if a large population is divided into a number of partially isolated subpopulations, migrations between the groups will eventually make all subpopulations have the same gene frequency q(imm), which then denotes the average for the entire population in the absence of other disturbing factors. If the local populations are differentiated genetically, there must be some mechanism (for example, local selection) to counteract the pooling effect of migrations so that an equilibrium condition may be reached. The change in gene frequency due to migration is independent of the mating system practiced in the population.
Mating systems
In a gene pool with respect to one locus, if a proportion p of the genes is A and a proportion q of the genes is a, the genotypic proportions in the population are still unknown until the mating pattern is specified. The mating pattern is a system by which the genes are associated into pairs to form the diploid genotypes. The mating systems vary widely in nature for different organisms and populations. Thus, wheat may have 1% cross-pollination and 99% self-fertilization, whereas maize practices the reverse. One of the simplest and most extensively studied systems is random mating, which is also known as panmixis.
Panmixis
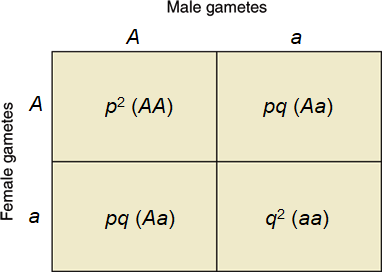
Random mating between individuals is equivalent to a random union of gametes. Thus, if the (pA, qa) gametes of one sex unite at random with the (pA, qa) gametes of the opposite sex, the resulting genotypic array will be p2(AA), 2pq(Aa), and q2(aa) [Fig. 2]. These genotypic proportions will be realized only in very large populations. See also: Hardy-Weinberg formula
Inbreeding
Inbreeding refers to mating between genetically related individuals. In cases of inbreeding, the frequency with which two A gametes unite will be greater than p2, and a similar situation is true for gene a. Consequently, inbreeding leads to an increase of homozygosis at the expense of heterozygosis.
Continued close inbreeding eventually leads to complete homozygosis. The population will then consist of pAA and qaa; that is, an A gamete will always unite with another A gamete, and an a gamete with another a gamete. Inbreeding between remote relatives does not necessarily lead to complete homozygosis, but only decreases the heterozygosis below the random mating level to a certain extent.
The inbreeding coefficient is an index intended to measure the amount or degree of inbreeding that has been accomplished in a population. Various indices may be constructed.
Genotype selective values
Within a large population, not all individuals produce the same number of offspring. In the situation to be considered, the average number of living offspring born to each of the genotypes in the population is studied, whereas random fluctuation in the number of offspring from family to family is ignored. Furthermore, it is assumed that the population is so large that only the relative frequencies of the various genotypes and genes in the population are of interest.
Natural selection
The doctrine of the survival of the fittest needs clarification from the genetic viewpoint. The relative genotypic reproductive values refer to the genetic composition of the offspring generation as it relates to that of the parent generation. These values include all causes for differential reproduction, such as fecundity, fertility, sexual maturity and capacity, survival and viability, length of reproductive life, and many others, depending on the details of the life cycle of the organism. In addition, the value, sometimes briefly referred to as relative fitness, is not necessarily correlated with any observable morphological characteristics, no matter how desirable that they may seem to humans. From the genetic viewpoint, only those who reproduce count. Thus, natural selection has no particular purpose, except to perpetuate those who are fit to reproduce under the given conditions. Only when a characteristic lowers the organism's reproductive capacity does it have a genetic effect on the subsequent generations.
Selection pressure and equilibrium
The effect of selection may be described in terms of changes in gene frequency. The population after selection is the parental population of the next generation through random mating.
Stability of an equilibrium
A stable equilibrium point leads to balanced genetic polymorphism, that is, to the coexistence of alleles in a population. Conversely, selection pressure against the heterozygote leads to the elimination of one of the alleles. In more complicated situations, there could be more than one stable or unstable equilibrium value in a population, or both. The study of selection effects may be extended to cases with multiple alleles, sex-linked alleles, autopolyploids, and inbreeding populations. See also: Polymorphism (genetics)
Gamete selection
The effective rate at which the A and a gametes function may not be the same; that is, selection may operate in the gametic stage instead of operating in the diploid genotypic stage. If the selective actions for the genotype aa, for example, and gamete a are in opposite directions, an equilibrium may result.
Random drift
The random drift (genetic drift) of gene frequencies in finite populations holds great significance (Fig. 3). The gene frequency of any generation is determined by the uniting gametes produced by the parents of the preceding generation. If the number of parents is limited and constitutes a random sample of the entire population, the gene frequency of the next generation will not remain exactly the same as that of the previous generation, but will be subject to a random fluctuation on account of the sampling process. In a random mating population of N individuals, one-half of whom are males and one-half females, and maintaining the same population size, the variance of the gene frequency based on 2N gametes is q(1 − q)/2N. The gene frequency may become a little higher or a little lower in the following generation—notably, the smaller the population, the greater is the variance. This random process will continue to operate in all generations. In a sufficiently long time, the value of q will reach either the terminal value 0 or 1. Hence, the random drift leads eventually to complete homozygosis for small populations. It also can be shown that the limiting rate of reaching the state 0 or 1 is ¼ per generation, so the total rate of "decay" of genetic variability is ½N per generation. Naturalists have found numerous small isolated colonies (for example, snails in mountain valleys) with characteristics uncorrelated with the environmental conditions to substantiate the theory of random (nonadaptive) fixation.
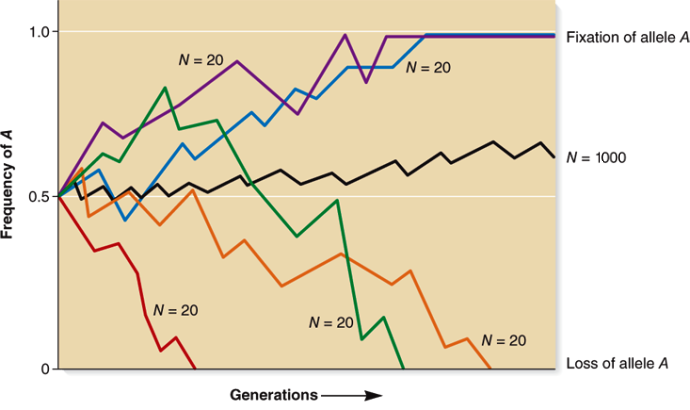
The effective size of a population is the actual number of individuals producing offspring and thereby responsible for the genetic constitution of the next generation. The random mating population with one-half males and one-half females, and producing the same number of offspring, is an idealized model. Any deviation from the ideal situation will have a different sampling variance and a different rate of decay. Equating these to the "standard" variance q(1 − q)/2N or the ideal decay rate ½N, an equivalent N is obtained for the ideal population. The latter number is known as the effective size of a population.
Distribution
A stationary distribution of gene frequencies results from two opposing forces—the systematic pressures (mutation, migration, and selection) that tend to make the gene frequency attain a certain fixed value, and the random variation due to sampling that tends to make the gene frequency drift away from any fixed value. The result of these opposing tendencies is not a single equilibrium value of gene frequency, but a stationary distribution of gene frequencies. This distribution may be viewed in three different ways—as the distribution of q for a particular locus in a population in a long period of time; as the distribution of the allelic frequencies of all loci subject to the same pressures in one population at any given time; and as the distribution of q of one locus among a large number of populations of the same size and with the same pressures at a given time.
Figure 4 shows some forms of the distribution under various conditions. The joint distribution of more than one locus is naturally very complicated. Furthermore, if the mutation rates and selection coefficients also vary instead of being constant, the mathematical description of the stochastic process becomes very laborious, and the forms shown in Fig. 4 give only a first approximation to the real situation.
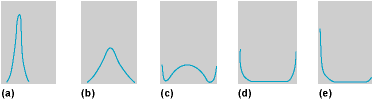
The distribution forms of the gene frequencies depend upon the relative magnitudes of the various factors that bring about populational changes. In large random-mating populations, all gene frequencies remain close to their stable equilibrium values, which are determined by the counteracting (but systematic) pressures of mutation, selection, and migration. There will be no further genetic change unless the environmental conditions change so as to define new equilibrium points. Evolution in such large populations is guided essentially by intragroup selection, and progress is very slow.
In small and completely isolated populations, most of the gene frequencies are close to 0 or 1 because of the random drift process that dominates the situation. Selection is ineffective, and the loci are prevented from being completely fixed by occasional mutations or immigrants. The ultimate fate of such small homozygous populations is probably extinction because they are nonadaptive and unable to respond to new conditions.
In populations of intermediate size, all factors—both random and systematic—come into play and the population is more responsive to evolutionary change. If a large population is subdivided into many partially isolated groups with migrations between them, there will be some differentiation among the groups. Some of it will be adaptive and some of it will be nonadaptive, but there is very little fixation. The selection effect, varying from one locality to another, then operates largely on an intergroup basis, which is more efficient than the intragroup selection within one single large population. If the groups are small, some of them will be eliminated by selection, whereas others will flourish. This provides the most favorable condition for evolutionary success for the species as a whole. The conclusion is that there is no one all-important factor in evolution. Evolutionary advance depends upon the interplay and balance of all factors.
Two-locus selection
All of the aforementioned properties apply strictly to one locus, or to independently distributed loci. When selection acts upon a two-locus genotype directly, the genes of two loci, linked or unlinked, are in general not independently distributed, even in a large random mating population. In selection involving more than one locus, it is inadequate to consider the gene frequencies at the various loci separately, and it is necessary to consider the gamete frequencies. In general, the lack of independence of genes at different loci renders the problem of natural selection and its evolutionary consequences far more complicated than is depicted by simple mathematical models.





