The process in which energy is removed from a beam of electromagnetic radiation and reemitted with a change in direction, phase, or wavelength. All electromagnetic radiation is subject to scattering by the medium (gas, liquid, or solid) through which it passes. In the short-wavelength, high-energy regime in which electromagnetic radiation is most easily discussed by means of a particle description, these processes are termed photon scattering. At slightly longer wavelengths, the scattering of x-rays provides the most effective means of determining the structure of crystalline solids. In the visible wavelength region, scattering of light produces the blue sky, red sunsets, and white clouds. At longer wavelengths, scattering of radio waves determines their characteristics as they pass through the atmosphere. See also: Light; Meteorological optics; Radio-wave propagation
It has been known since the work of J. Maxwell in the nineteenth century that accelerating electric charges radiate energy and, conversely, that electromagnetic radiation consists of fields which accelerate charged particles. Light in the visible, infrared, or ultraviolet region interacts primarily with the electrons in gases, liquids, and solids—not the nuclei. The scattering process in these wavelength regions consists of acceleration of the electrons by the incident beam, followed by reradiation from the accelerating charges. See also: Electromagnetic radiation
Scattering processes may be divided according to the time between the absorption of energy from the incident beam and the subsequent reradiation. True “scattering” refers only to those processes which are essentially instantaneous. Mechanisms in which there is a measurable delay between absorption and reemission are usually termed luminescence. If the delay is longer than a microsecond or so, the process may be called fluorescence; and mechanisms involving very long delays (seconds) are usually termed phosphorescence. See also: Absorption of electromagnetic radiation; Fluorescence; Luminescence; Phosphorescence
Inelastic scattering
Instantaneous scattering processes may be further categorized according to the wavelength shifts involved. Some scattering is “elastic”; there is no wavelength change, only a phase shift. In 1928 C. V. Raman discovered the process in which light was inelastically scattered and its energy was shifted by an amount equal to the vibrational energy of a molecule or crystal. Such scattering is usually called the Raman effect. This term has been used in a more general way, however, often to describe inelastic scattering of light by spin waves in magnetic crystals, by plasma waves in semiconductors, or by such exotic excitations as “rotons,” the elementary quanta of superfluid helium. See also: Raman effect
Brillouin and Rayleigh scattering
In liquids or gases two distinct processes generate inelastic scattering with small wavelength shifts. The first is Brillouin scattering from pressure waves. When a sound wave propagates through a medium, it produces alternate regions of high compression (high density) and low compression (or rarefaction). A picture of the density distribution in such a medium is shown in Fig. 1. The separation of the high-density regions is equal to one wavelength λ for the sound wave propagating. Brillouin scattering of light to higher (or lower) frequencies occurs because the medium is moving toward (or away from) the light source. This is an optical Doppler effect, in which the frequency of sound from a moving object is shifted up in frequency as the object moves toward the observer. See also: Doppler effect
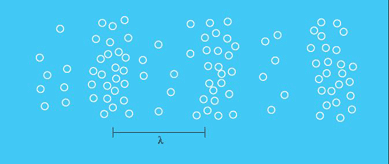
The second kind of inelastic scattering studied in fluids is due to entropy and temperature fluctuations. In contrast to the pressure fluctuations due to sound waves, these entropy fluctuations do not generate scattering at sharp, well-defined wavelength shifts from the exciting wavelength; rather, they produce a broadening in the scattered radiation centered about the exciting wavelength. This is because entropy fluctuations in a normal fluid are not propagating and do not, therefore, have a characteristic frequency; unlike sound they do not move like waves through a liquid—instead, they diffuse. Under rather special circumstances, however, these entropy or temperature fluctuations can propagate; this has been observed in super-fluid helium and in crystalline sodium fluoride at low temperatures, and is called second sound. See also: Entropy; Second sound
Scattering from entropy or temperature fluctuations is called Rayleigh scattering. In solids this process is obscured by scattering from defects and impurities. Under the assumption that the scattering in fluids is from particles much smaller than the wavelength of the exciting light, Lord Rayleigh derived in 1871 an equation, shown below,
for such scattering; here I(θ) is the intensity of light scattered from an incident beam of wavelength λ and intensity I0 at a distance r; d is the number of scattering particles; υ is the volume of the disturbing particle; and n is the index of refraction of the fluid. The cos θ term is present for unpolarized incident light, where θ is the scattering angle. Measurement of the ratio in Rayleigh's equation allows the determination of either Avogadro's number N or the molecular weight M of the fluid, if the other is known. The dependence of scattering intensity upon the inverse fourth power of the wavelength given in Rayleigh's equation is responsible for the fact that daytime sky looks blue and sunsets red: blue light is scattered out of the sunlight by the air molecules more strongly than red; at sunset, more red light passes directly to the eyes without being scattered.
Large particles
Rayleigh's derivation of his scattering equation relies on the assumption of small, independent particles. Under some circumstances of interest, both of these assumptions fail. Colloidal suspensions provide systems in which the scattering particles are comparable to or larger than the exciting wavelengths. Such scattering is called the Tyndall effect and results in a nearly wavelength-independent (that is, white) scattering spectrum. The Tyndall effect is the reason clouds are white (the water droplets become larger than the wavelengths of visible light). See also: Tyndall effect
The breakdown of Rayleigh's second assumption—that of independent particles—occurs in all liquids. There is strong correlation between the motion of neighboring particles. This leads to fixed phase relations and destructive interference for most of the scattered light. The remaining scattering arises from fluctuations in particle density discussed above and was first analyzed theoretically by A. Einstein in 1910 and by M. Smoluchowski in 1908.
Rayleigh's basic theory has been extended by several authors. Rayleigh in 1911 and R. Gans in 1925 derived scattering formulas appropriate for spheres of finite size, and in 1947 P. Debye extended the theory to include random coil polymers. The combined results of these three workers, generally called the Rayleigh-Gans-Debye theory, is valid for any size of particle, provided the refractive index n is near unity; whereas the Rayleigh theory is valid for any index, provided the particles are very small. The index n of any medium would be unity if there were no scattering.
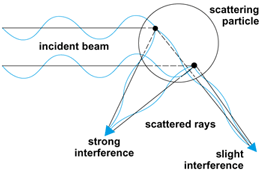
A more complete theory than Rayleigh-Gans-Debye was actually developed earlier by G. Mie in 1908; however, Mie's theory generally requires numerical solution. Mie's theory is valid even for particles larger than the wavelength of light used. For such particles large phase shifts occur for the scattered light. Mie scattering exhibits several maxima and minima as a function of scattering angle; the positions of these maxima depend upon particle size, as indicated in Fig. 2. These secondary maxima are essentially higher-order Tyndall scattering.
Critical opalescence
The most striking example of light scattering is that of critical opalescence, discovered by T. Andrews in 1869. As the critical temperature of a fluid is approached along the critical isochore, fluctuations in the density of the medium become larger than a wavelength and stay together for longer times. The independent particle approximation becomes very bad, and the intensity of light scattered in all directions becomes very large. The fluid, which might have been highly transparent at a temperature 1°C (1.8°F) higher, suddenly scatters practically all of the light incident upon it. The regions of liquidlike density in the fluid have molecules moving in phase, or “coherently,” within them. Such coherent regions in fluids near their critical temperatures behave very much like the large spherical particles diagrammed in Fig. 2, thus establishing the relationship between Mie scattering of colloids and critical opalescence. The theory of scattering from correlated particles was developed primarily by L. S. Ornstein and F. Zernike in 1914–1926. See also: Coherence; Critical phenomena; Opalescence
Nonlinear scattering
At the power densities available with pulsed lasers, a variety of other scattering mechanisms can become important. (For nonlaser excitation these processes exist but are generally too weak to be detected.) Such processes include second-harmonic generation, in which the energy from two quanta (photons) in the incident beam produces one doubly energetic photon. A practical example is the production of green light from the red light of a ruby laser. Third-harmonic generation (and similar higher-order processes) also occurs as an intense scattering mechanism at sufficiently high power densities. Whereas second-harmonic generation can occur only in certain crystals, for reasons of symmetry, third-harmonic generation occurs in any medium. Other more exotic nonlinear scattering mechanisms include sum generation and difference generation, in which two beams of light are combined to produce scattering having frequencies which are the sum or difference of the frequencies in the two incident beams, and rather weak processes such as the hyper-Raman effect, in which the scattered light has a frequency which is twice that of the incident beam plus (or minus) some vibrational energy. These effects are nonlinear because their intensities vary according to the square or higher power of the incident intensity. These nonlinear processes may be very important in astrophysics (for example, in stellar interiors), in addition to laboratory laser experiments. See also: Nonlinear optics





