Key Concepts
Construction of a mathematical model of the climate system of the Earth capable of simulating its behavior under present and altered conditions. The Earth's climate is continually changing over time scales ranging from hundreds of years to a few years. Since the climate is determined by the laws of classical physics, it should be possible in principle to construct such a model (Fig. 1). The advent of a worldwide weather-observing system capable of gathering data for validation and the development and widespread routine use of digital computers have made this undertaking possible, starting in the mid-1970s.
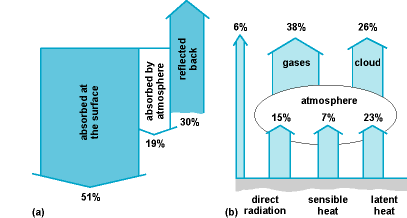
The first attempts at modeling the planetary climate showed that the Earth's average temperature is determined mainly by the balance of radiant energy absorbed from sunlight and that emitted by the Earth system. About 30% of the incoming radiation is reflected directly to space, and 72% of the remainder is absorbed at the surface (Fig. 2). The incoming solar radiation is divided among reflection, absorption by the atmospheric constituents, and absorption by the surface of the planet. The outgoing infrared radiation comes from the surface, atmospheric gases, and clouds. In addition, the atmosphere radiates down to the surface, and the surface gives energy to the atmosphere in the forms of latent and sensible heat. The radiation is absorbed unevenly over the Earth, which sets up thermal contrasts that in turn induce convective circulations in the atmosphere and oceans. Climate models attempt to calculate from mathematical algorithms the effects of these contrasts and the resulting motions in order to understand better and perhaps predict future climates in some probabilistic sense. See also: Solar radiation; Terrestrial radiation
Climate models differ in complexity, depending upon the application. The simplest models are intended for describing only the surface thermal field at a fairly coarse resolution. These mainly thermodynamical formulations are successful at describing the seasonal cycle of the present climate, and have been used in some simulations of past climates, for example, for different continental arrangements that occurred millions of years ago. At the other end of the spectrum are the most complex climate models, which are extensions of the models used in weather forecasts. These models aim at simulating seasonal and even monthly averages just shortly into the future, based upon conditions such as the temperatures of the tropical-sea surfaces. Intermediate to these extremes are models that attempt to model climate on a decadal basis, and these are used mainly in studies of the impact of anthropogenically induced climate change. See also: Climate modification
Climate models are used in a large variety of applications that aid in the understanding of Earth history. Many simple climate model simulations have been used to sort out the mechanisms responsible for climate change in the past. For example, although not yet fully understood, the astronomical theory of the ice ages states that the waxing and waning of the great continental ice sheets has been forced by the periodic changes in the Earth's elliptical orbit parameters in the past. Similarly, the onset of glaciation in Antarctica and Greenland has been studied by such means. See also: Climate history
A problem that has received considerable attention is the greenhouse effect. Models are studied to achieve better understanding of how the increase of atmospheric carbon dioxide and other trace gases from anthropogenic sources is likely to change the climate in the coming decades. The models are compared to past climates ranging from the ice ages to the records of the last hundred years, for which an instrumental record exists. See also: Greenhouse effect
Anatomy of models
Since the main interest of climate modelers is in computing the thermal field over the Earth, a primary objective is to represent the conservation of energy at each location in the system. One requirement is accurate formulations of the absorption and reflection of solar radiation as it passes through the atmosphere and strikes surfaces. Another is the radiation emitted from each mass element in the Earth-atmosphere system. Conversions of heat from latent to sensible must be taken into account as water changes its phase in the system. Clouds must be included since they participate in the radiation transfer and in the changes of water phase. Similarly, snow and ice cover enter both energy disposal accounts. The thermodynamic expression of the conservation of energy is not complete until allowance is made for the flow of matter of a different temperature into a given region. To include this effect, a model of the circulation must be considered, and this in turn is governed by the same thermal contrasts given by the thermodynamic equation.
The circulation of atmospheric and oceanic material is governed by Newton's second law: local acceleration of a fluid element is proportional to total forces on it. In fluid mechanics this is known as the Navier-Stokes equation. It is a nonlinear partial differential equation that is exceedingly complex. Climate models that include a detailed attempt to solve the fluid dynamics equations must be approached by computer simulation. Even here the solutions are known to differ in detail from nature after only a few weeks at most. However, it is thought that statistics, for example, long-term means for the climate of the numerical model and those of nature, should agree; and this has been borne out in numerous tests. See also: Navier-Stokes equation; Simulation
Simulation models which include ocean circulation are important in understanding the adjustment processes in going from one climate state to another. Inclusion of the ocean dynamics adds significantly to the computational burden, since a finer grid is required owing to the importance of small-scale motions. The irregularity of the bottom topography also complicates the problem.
Feedback mechanisms and sensitivity
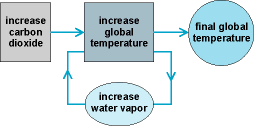
Attempts at modeling climate have demonstrated the extreme complexity and subtlety of the problem. This is due largely to the many feedbacks in the system. One of the simplest and yet most important feedbacks is that due to water vapor. If the Earth is perturbed by an increase in the solar radiation, for example, the first-order response of the system is to increase its temperature. But an increase in air temperature leads to more water vapor evaporating into the air; this in turn leads to increased absorption of space-bound long-wave radiation from the ground (greenhouse effect), which leads to an increased equilibrium temperature. This effect, known as a positive-feedback mechanism, is illustrated in Fig. 3. Water vapor feedback is not the only amplifier in the system. Another important one is snow cover: a cooler planet leads to more snow and hence more solar radiation reflected to space, since snow is more reflecting of sunlight than soil or vegetation. Other, more subtle mechanisms that are not yet well understood include those involving clouds, oceans, and the biosphere.
While water vapor and snow cover feedback are fairly straightforward to model, the less understood feedbacks differ in their implementations from one climate model to another. These differences as well as the details of their different numerical formulations have led to slight differences in the sensitivity of the various models. All models agree that the planetary average temperature should increase if carbon dioxide concentrations increase. The predicted response in planetary temperatures ranges 0.5 to 8.6°F (0.3 to 4.8°C) by 2100. See also: Meteorological satellites
Atmosphere-ocean-land models
Simulating the naturally varying present-day climate and its future evolution can be accomplished only with coupled atmosphere-ocean-land models.
Atmosphere models
Numerical models of the atmosphere are used to reveal its underlying dynamics and to predict the weather. The climatic application of models requires a knowledge of the change in lower-boundary conditions as the model evolves in time: over the oceans, sea surface temperature; and over land, more complex descriptors of the land surface.
Both the ocean and land interact with the atmosphere on multiple time scales. Ocean interactions depend on the thermal capacities of water columns that undergo rapid vertical exchanges, usually about 165–3300 ft (50–1000 m) of water. An unchanging field of sea surface temperature may be used as a model boundary to predict weather a few days in advance (at most) because the huge thermal capacities of the oceans cause hardly any change in the bottom boundary. Dry land, however, interacts with the atmosphere with effective heat capacities of a fraction of a meter of water, so that large thermal variations in interaction with the atmospheric boundary occur over time scales as short as the diurnal cycle. Longer time scales occur for moist soils: for example, soil moisture stores may require several weeks to be depleted. Also, the atmosphere above the boundary layer may require several weeks to be influenced by the underlying boundaries. For simulations or predictions beyond a week, the correct time evolution of the bottom boundary conditions for sea surface temperature and land soil moisture must be calculated.
Coupled models
To consistently simulate both atmospheric and boundary quantities, it is necessary to couple the media and allow them to mutually and consistently evolve. Even to predict evolution of the atmosphere alone, climate models must be coupled atmosphere-ocean-land models.
Numerical models of the ocean are used to understand its underlying dynamics and to predict the sea surface temperature. For these purposes, the fluxes of heat and momentum from the atmosphere must be specified. On sufficiently long time scales, the atmosphere requires sea surface temperatures from the ocean, and the ocean requires momentum and heat fluxes from the atmosphere. Numerical models of the land are used to study basic hydrological processes and to predict temperature, stored moisture, and runoff. Fluxes of heat and water from the atmosphere must be specified because the atmosphere requires land properties and the land requires atmospheric fluxes. Many atmospheric processes must be adequately simulated in order to correctly supply the fluxes of heat, momentum, and moisture to the ocean and to the land surfaces, for example, those processes involving rainfall, cloud optical properties, surface winds, radiation, and atmospheric temperature. These variables, in turn, are affected by the properties of the underlying surface.
Sensitivity studies
Significant properties of the ocean and land components of coupled climate models can be tested and demonstrated by the use of sensitivity studies. These studies assume simple changes in model parameters and assess the significance of the responses. They have demonstrated that changes in surface boundary conditions can have a profound influence on regional rainfall patterns and intensities and can also determine the specifics of how the surface conditions influence atmospheric precipitation.
Surface-precipitation interactions are affected by the heat and moisture supplied by the lower boundary to the planetary boundary layer. Moist convection occurs when an atmospheric column is unstable with respect to a parcel of boundary layer air. Wetter and warmer surfaces promote this instability, as does colder air in the overlying atmosphere. Convection occurring in one location acts to warm and stabilize the atmosphere elsewhere. Therefore, convective rainfall in one location can suppress convection elsewhere. Over land, the diurnal cycle of solar heating promotes the greatest convective instability in the afternoon. Over oceans, warmest sea surface temperatures usually, but not always, produce the greatest convective instabilities. Climate model simulations can test their treatment of surface coupling through comparisons of the simulated and observed diurnal variations of rainfall. These diurnal variations are especially pronounced over land, but they are also notable over the tropical oceans. For example, a model with initially dry soil predicts substantially lower summer convective rainfall in subsequent days, or even weeks, than does a model with initially wet soil. See also: Convective instability
Uses of coupled models
Coupled atmosphere-ocean-land models are used to simulate climate over time scales of longer than a few weeks. These models are used to predict future natural variations (that is, variations that occur without human-induced changes of the gas and aerosol composition of the atmosphere) or to project responses to human-induced changes such as the addition of greenhouse gases.
One natural variation is El Niño, the complex of phenomena connected with warm sea surface temperature in the eastern and central tropical Pacific that seems to occur on an irregular 4-year time scale. By limiting the active extent of the coupled models to the tropical Pacific, high resolution can be attained and predictions of El Niño using such models become possible. Data in the tropical Pacific are used to initialize the forecast, that is, to specify the initial internal state of the upper ocean. The coupled model is then allowed to run freely, and the future evolution of the entire system is predicted. Used in this way, coupled models have provided predictions up to a year in advance that have been useful in making economic decisions in nations bordering the tropical Pacific. See also: El Niño; Tropical meteorology
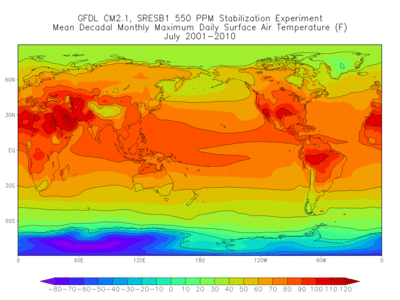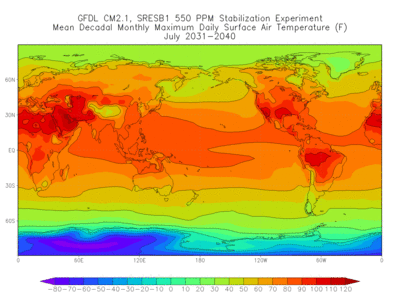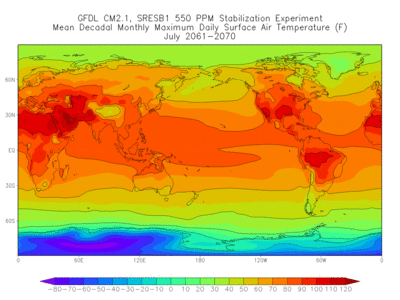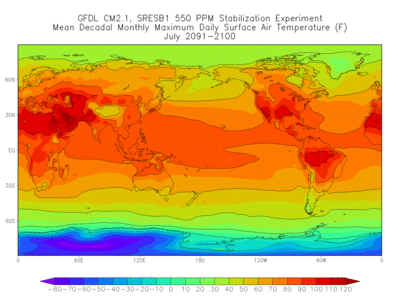
In terms of human-induced changes, coupled atmosphere-ocean-land models are used to project a climatic response to the increase of greenhouse gases. To project what the climatic response would be to an increase of greenhouse gases, the present climate must first be simulated. Next, an assumption must be made that the composition of the atmosphere will change in a specified way; for example, it may be assumed that carbon dioxide will increase by 1% per year. Atmosphere-ocean-land models of long-term response to the anthropogenic addition of atmospheric gases have indicated that carbonaceous and sulfate aerosols have a major cooling affect (by direct blocking of the Sun's rays) on regions of the Earth's surface local to the emissions of such constituents. They may also have an indirect cooling effect by acting as cloud condensation nuclei to increase the amount of cloud cover. Projections of the climatic response to additions of greenhouse gases must include the effects of aerosols. See also: Climatic prediction; Climatology; Weather forecasting and prediction
Uncertainties in climate models
Because the Earth's climate is far too complex to reproduce in a laboratory, scientists have developed numerical climate models, based on the conservation of energy, momentum, and mass, which can be used to simulate past, present, and future climate conditions. These models incorporate the key physical parameters and processes that govern the climate behavior. Climate models that simulate the entire global atmosphere are called general circulation models (GCMs). Those models applied to a limited domain are called regional climate models (RCMs). The horizontal resolution of most general circulation models is 100 km (60 mi) or larger. Regional climate models have a horizontal resolution of a few tens of kilometers, but the initial and lateral boundary conditions of the RCMs depend upon the GCM output or reanalysis, which is a combination of the GCMs' output and observations. Consequently, RCMs may have more detailed physics and finer resolution, but the uncertainties of the GCM may pass to the RCMs through initial and/or boundary conditions when the RCM is used to predict the future climate.
Climate models (referring to atmospheric models coupled with ocean and land-soil models, hereafter) can be used to simulate changes in temperature, rainfall, snow cover, winds, soil moisture, sea ice, and ocean circulations for periods from seasons to decades. However, the mathematical models used are obviously simplified versions of the real Earth and cannot capture its full complexity. The nonlinear partial differential equations of the climate systems (that is, Navier-Stokes equations) cannot be solved analytically. In climate models, these equations are converted into the discrete difference equations in both time and space and solved numerically. Many numerical schemes and grid structures have been developed and applied in climate models to obtain the approximate numerical solutions. Theoretically, the numerical solutions should converge to the analytical (or true) solutions, but the accuracy can quickly deteriorate as the number of integrations increases in a model using coarse resolution, inappropriate numerical schemes, or improper grid structure. The discrete mode of the solutions also imposes a constraint that the smallest element that can be resolved by the model is twice the resolution (2Δ). The nonlinear terms of the Navier-Stokes equations can generate waves shorter than 2Δ. Those short waves can be misrepresented as the resolvable waves (that is, aliasing), causing nonlinear instability. Artificial filters or smoothing (which can also be generated by truncation errors of the numerical schemes) have been applied to control these instabilities.
Because of the resolution, climate models cannot resolve individual clouds, small-scale turbulence, detailed features of complex terrain, soil properties, or land distributions. They are called the subgrid-scale properties. The effect of the subgrid-scale properties should be formulated by parametrizations. For example, the effect of the subgrid-scale clouds is assumed as a function of the moisture convergence and other fields, which can be resolved by the models. Meteorologists have proposed various cumulus parametrizations to represent the effect of the subgrid-scale clouds; however, it is very difficult to formulate the cumulus parametrizations or other subgrid-scale features based on rigorous mathematics and physics. Models with a fine resolution can resolve the majority of the flow explicitly and reduce the spurious contributions from the subgrid-scale features. But the subgrid-scale parametrizations are still important, even in J. W. Deardorff's large-eddy simulation of a convective boundary layer with a model resolution of 50 m (160 ft). Subgrid-scale features and short-wave disturbances may affect the large-scale weather/climate pattern through the nonlinear terms of the equations.
Uncertainties also exist in formulating cloud physics, radiation, ocean current, and the effects of aerosol, as well as snow-land-surface, air-sea, sea-ice interactions. For example, using the same observed data as the initial conditions, a comparison of the snow-land-surface models shows considerable variation among the results, and most were unable to reproduce the observations due to deficiencies in numerical schemes, physics, or model resolution. For this reason, land models need to be refined before they can appropriately represent the effect of the soil and snow in a climate system. Better parametrizations in cloud physics, turbulence, radiation, aerosols, sea-ice and air-sea interactions, as well as finer model resolution are required in most models. See also: Cloud physics
The accuracy of the initial conditions is very important for numerical weather forecasting. The initial conditions for a GCM come from the reanalysis, which combines observations and model results, both of which may contain errors. The errors of observations may come from instruments or interpretation errors in both time and space. The sources of errors from modeling may be due to numerical schemes, physics, resolution, as well as initial and boundary conditions used in the model. These errors may be amplified or suppressed during the climate model integration. The result of the numerical simulations can become quite different from the observation after just 1 or 2 weeks.
Since uncertainty always exists in a numerical weather prediction model, scientists have applied ensemble-forecasting techniques. The ensemble method may include running the same model with different initial and boundary conditions (for example, to disturb the initial conditions or to start to integrate the model at different times), running several different models with the same initial/boundary conditions, or running different models with different initial/boundary conditions to estimate the probability of the model forecasting. If the results diverge, the confidence of the results is low; otherwise, the confidence is high. There is no guarantee that the real climates are completely covered by the model results. For example, if all of the models are deficient in describing specific physical process, the ensemble average of these models will also be deficient. The model also may not be able to predict extreme cases, which are needed most.
If a model can reasonably simulate the current weather and produce good short-term forecast (7–14 days), it has a better chance to predict future climate change or simulate the past climate because the climate is an accumulation of daily weather processes. A model with more detailed physics, finer resolutions, and more accurate numerical schemes and initial/boundary conditions usually performs better. Although an RCM can simulate the observations reasonably well even after a few years integration when reanalysis is used as the initial/lateral boundary conditions, it cannot be used alone to predict the climate in the future without coupling with a GCM. On the other hand, it is unlikely that GCM-simulated weather systems will compare favorably with observations after a few weeks of integration. Climate studies usually emphasize statistics instead of describing any single weather event. The climate simulations also depend more on the boundary conditions, which include solar radiation and properties of the soil and ocean, than the initial conditions. Currently, many climate models are being used to simulate the climate in the future or the past. For example, the climate models show that the mean atmosphere becomes warmer under the doubled atmospheric carbon dioxide (CO2) scenario, with quite different regional responses. When climate models are applied to forecast the future climate, they also encounter uncertainties in volcanic activity, forest fires, the change of trace gases/aerosols and emission, and the change of vegetation and land surface due to human activities.





