Key Concepts
The time rate of change of velocity. Acceleration is a physics term that measures the rate of change of velocity per unit of time. Because velocity is a directed or vector quantity involving both magnitude and direction, a velocity may change by a change of magnitude (speed) or by a change of direction, or both. It follows that acceleration is also a directed, or vector, quantity (Fig. 1). See also: Acceleration analysis; Acceleration measurement; Accelerometer; Speed; Velocity
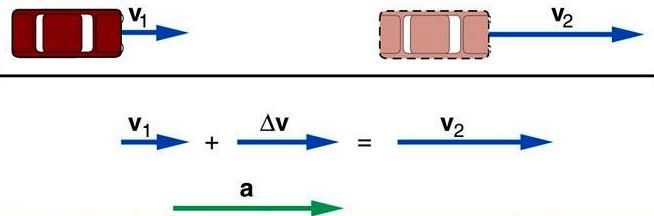
If the magnitude of the velocity of a body changes from v1 ft/s to v2 ft/s in t seconds, then the average acceleration has a magnitude given by equation (1):
To designate it fully, the direction should be given, as well as the magnitude.
Instantaneous acceleration is defined as the limit of the ratio of the velocity change to the elapsed time as the time interval approaches zero. When the acceleration is constant, the average acceleration and the instantaneous acceleration are equal.
If a body, moving along a straight line, is accelerated from a speed of 10 to 90 ft/s (3 to 27 m/s) in 4 s, then the average change in speed per second is (90 – 10)/4 = 20 ft/s or (27 – 3)/4 = 6 m/s in each second. This is written 20 ft per second per second or 20 ft/s2, or 6 m per second per second or 6 m/s2. Accelerations are commonly expressed in feet per second per second, meters per second per second, or any similar units.
Whenever a body is acted upon by an unbalanced force, it will undergo acceleration. If it is moving in a constant direction, the acting force will produce a continuous change in speed. If it is moving with a constant speed, the acting force will produce an acceleration consisting of a continuous change of direction. In the general case, the acting force may produce both a change of speed and a change of direction. See also: Force
Angular acceleration
Angular acceleration is a vector quantity representing the rate of change of angular velocity of a body experiencing rotational motion. If, for example, at an instant t1, a rigid body is rotating about an axis with an angular velocity ω1, and if, at a later time t2, it has an angular velocity ω2, the average angular acceleration (which is expressed in radians per second per second) is given by equation (2):
The instantaneous angular acceleration is given by α = dω/dt.
Consequently, if a rigid body is rotating about a fixed axis with a constant angular acceleration of magnitude α and an angular speed of ω0 at a given time, then the angular speed at a later time t is given by equation (3):
A simple calculation shows that the angular distance θ traversed in this time is expressed by equation (4):
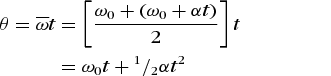 (4)
(4)In Fig. 2, a particle is shown moving in a circular path of radius R about a fixed axis through O with an angular velocity of ω radians/s and an angular acceleration of α radians/s2. This particle is subject to a linear acceleration that, at any instant, may be considered to be composed of two components: a radial component ar and a tangential component at. See also: Rotational motion
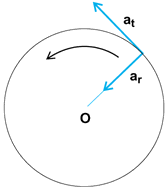
Radial acceleration
When a body moves in a circular path with constant tangential speed at each point in its path, it is also being constantly accelerated toward the center of the circle under the action of the force required to constrain it to move in its circular path. This acceleration toward the center of path is called radial acceleration. In Fig. 2, the radial acceleration, sometimes called centripetal acceleration, is shown by the vector ar. The magnitude of its value is v2/R, or ω2/R, where v is the instantaneous tangential velocity. This centrally directed acceleration is necessary to keep the particle moving in a circular path. See also: Centripetal force
Tangential acceleration
The component of linear acceleration tangent to the path of a particle subject to an angular acceleration about the axis of rotation is called tangential acceleration. In Fig. 2, the tangential acceleration is shown by the vector at. The magnitude of its value is αR.





