Key Concepts
A nuclear reaction that combines low-mass, colliding nuclei into moderate-mass elements and liberates a great deal of energy in the process. Nuclear fusion is a very important process for nucleosynthesis of the elements and for producing energy in stars, the hydrogen bomb, and potentially in thermonuclear power reactors. See also: Hydrogen bomb; Nucleosynthesis; Stellar evolution
Fusion is the primary nuclear reaction for nuclei with less than approximately 60 nucleons (protons and neutrons); that is, the nuclei in which the binding energy per nucleon generally increases with increasing number of nucleons (Fig. 1). See also: Atomic nucleus; Nuclear reaction; Nucleon
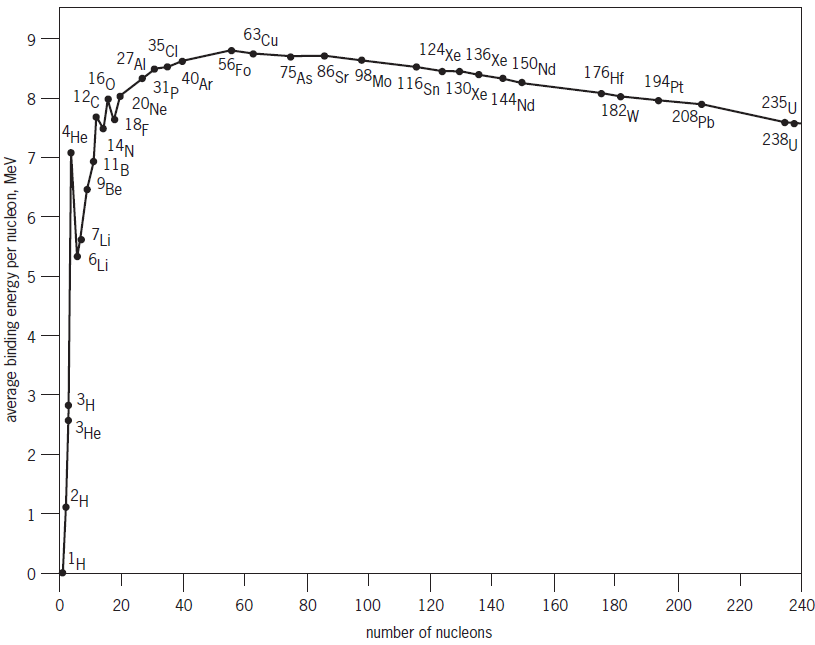
The energy that must be added to break the nucleus into its individual components, and which is equal to the energy that is released when the nucleus is formed, is known as the binding energy. The sum of the binding energies of the nuclei going into a collision less the sum of the binding energies of the nuclei coming out of the collision is the energy released in a fusion reaction. The binding energy is typically many megaelectronvolts (MeV) and is about 1000 times more than the typical energy release of a chemical reaction. See also: Nuclear binding energy
The higher the binding energy of a nucleus, the more likely that nucleus will form in a collision. By this process, very-low-mass nuclei, such as the hydrogen and helium nuclei that formed in the first 300 seconds of the universe, combine to form nuclei with up to 60 nucleons. Fusion is one of the primary processes for nucleosysnthesis of the elements. See also: Big bang theory; Universe
The fusion process is not to be confused with fission, which is the primary nuclear reaction for nuclei with more than about 60 nucleons, for which the binding energy per nucleon generally decreases with increasing number of nucleons (Fig. 1). Fission reactions break very massive nuclei into smaller nuclei—exactly the opposite of fusion—while liberating energy for atomic bombs, fission power reactors, and nuclear medicine. See also: Nuclear fission
The fusion reaction is also not to be confused with the very energetic nuclear collisions in high-energy physics accelerators such as the Large Hadron Collider, in which nucleons are broken apart into their component quarks to form different particles.
Promise and challenge of fusion energy
Because a primary fusion fuel, deuterium, is available in virtually inexhaustible supply in seawater (with an abundance of 1 atom of deuterium occurring per 6500 atoms of hydrogen), an economically attractive fusion power system would solve the problem of depleting fossil fuels as chemical energy sources. The corresponding reduction of carbon dioxide (CO2) emissions would also help mitigate the problem of climate change, especially if electric cars replace gasoline-powered cars for motorized transport. The lack of radioactive waste products from the fusion reaction, compared to those of the fission of uranium in today's nuclear reactors, is another argument in this mode of power generation's favor. See also: Climate modification; Deuterium; Energy sources; Nuclear power; Radioactive waste management; Spent nuclear fuel disposition
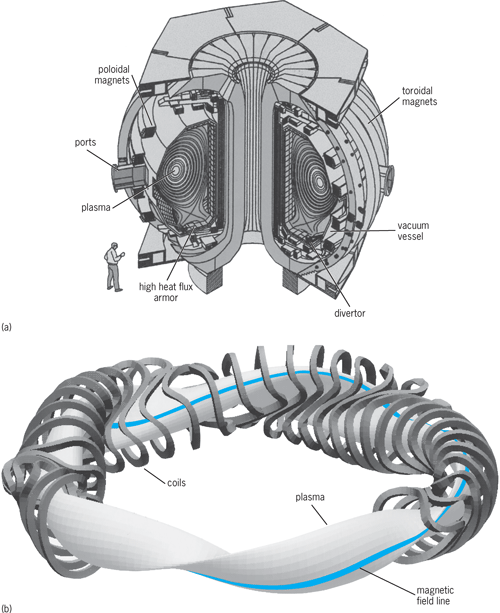
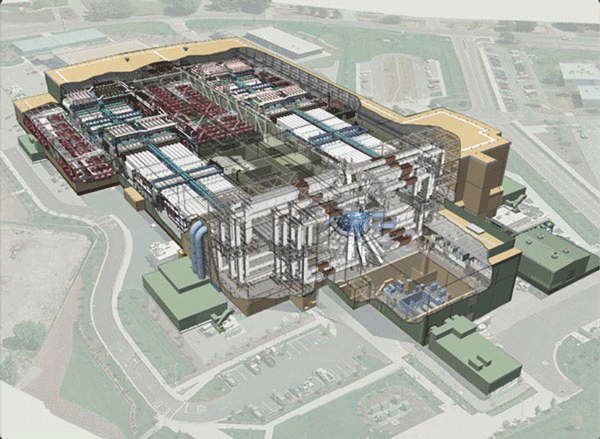
Unfortunately, an economically attractive and socially acceptable fusion energy solution is a very difficult challenge. However, the current and expected availability of new facilities of unprecedented scale for the traditional approaches in both magnetic confinement fusion (Fig. 2) and inertial fusion confinement fusion (Fig. 3), and investments by private industry in several innovative approaches to fusion, are encouraging. See also: Inertial confinement fusion; Magnetic confinement fusion; Muon-catalyzed fusion
Properties of fusion reactions
In a nuclear fusion reaction, the close collision of two energy-rich nuclei results in a mutual rearrangement of their nucleons to produce two or more reaction products, together with a release of energy. The energy from fusion usually appears in the form of kinetic energy of the reaction products, although when energetically allowed, part of the energy may be taken up as energy of an excited state of a product nucleus. In contrast to neutron-produced fission reactions, positively charged colliding nuclei in fusion reactions require a substantial initial relative kinetic energy to overcome their mutual electrostatic repulsion so that the nuclei can get close enough to react. This required relative energy increases with the nuclear charge Z, so that reactions between low-Z nuclei are the easiest to produce. The best known of these are the reactions between the heavy isotopes of hydrogen, which are deuterium (D) and tritium (T). In addition, the continuing lack of a socially accepted method for disposing of radioactive waste has stimulated new interest in the more challenging fusion reactions that use deuterium with helium containing only one neutron (D 3He) and protons (H) with boron (H 11B). See also: Tritium
Fusion reactions were discovered in the 1920s when low-Z elements were used as targets and bombarded by beams of energetic protons or deuterons. However, the nuclear energy released in such bombardments is always microscopic compared with the energy of the impinging beam. This is because most of the energy of the beam particle is dissipated uselessly by ionization and interparticle collisions in the target; only a small fraction of the impinging particles actually produces reactions.
Nuclear fusion reactions can be self-sustaining, however, if they are carried out at a very high temperature. That is, if the fusion fuel exists in the form of a very hot ionized gas consisting of stripped nuclei and free electrons, termed a plasma, the agitation energy of the nuclei can overcome their mutual repulsion, causing reactions to occur. This is the mechanism of energy generation in the stars and in the fusion bomb. It is also the method envisaged for the controlled generation of fusion energy. See also: Plasma (physics)
Simple reactions
The cross sections (effective collisional areas) for many of the simple nuclear fusion reactions have been measured with high precision. It is found that the cross sections generally show broad maxima as a function of energy and have peak values in the general range of 0.01 barn (1 barn = 10−28 m2) to a maximum value of 5 barns, for the deuterium–tritium reaction. The energy released in these reactions can be readily calculated from the mass differences between the initial and final nuclei or determined by direct measurement.
Some of the important fusion reactions for terrestrial energy production, their reaction products, and their energy releases are given by reactions (1).
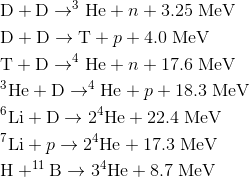 (1)
(1)The energy released in a chemical reaction, such as hydrogen and oxygen combining to produce a water molecule, is about 1 eV per reaction, so fusion fuel releases more than a million times as much energy per gram as typical chemical fuels.
The two alternative D–D reactions listed occur with about equal probability for the same relative particle energies. The heavy reaction products, tritium and helium-3, may also react, with the release of a large amount of energy. Thus it is possible to visualize a reaction chain in which six deuterons are converted to two helium-4 nuclei, two protons, and two neutrons, with an overall energy release of 43 MeV—about 100,000 kWh of energy per gram of deuterium. This energy release is several times that released per gram in the fission of uranium, and several million times that released per gram by the combustion of gasoline.
Cross sections
Figure 4 shows the measured values of cross sections as a function of bombarding energy up to 100 keV for the total D–D reaction (both D–D, n and D–D, p), the D–T reaction, and the D–3He reaction. The most striking characteristic of these curves is their extremely rapid falloff with energy as bombarding energies drop to a few kilovolts. This effect arises from the mutual electrostatic repulsion of the nuclei, which prevents them from approaching closely if their relative energy is small. See also: Nuclear structure
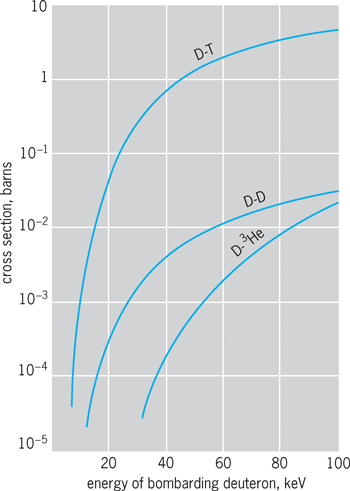
The fact that reactions can occur at all at these energies is attributable to the finite range of nuclear interaction forces. In effect, the boundary of the nucleus is not precisely defined by its classical diameter. The role of quantum-mechanical effects in nuclear fusion reactions has been treated by G. Gamow and others. It is predicted that the cross sections should obey an exponential law at low energies. This is well borne out in energy regions reasonably far removed from resonances (for example, below about 30 keV for the D–T reaction). Over a wide energy range at low energies, the data for the D–D reaction can be accurately fitted by a Gamow curve, the result for the cross section being given by Eq. (2),
where the bombarding energy W is in kiloelectronvolts; 1 keV kinetic temperature = 11.6 million degrees K.
The extreme energy dependence of this expression can be appreciated by the fact that between 1 and 10 keV the predicted cross section varies by about 13 powers of 10, that is, from 2 × 10−46 to 1.5 × 10−33 m2.
Reaction rates
When nuclear fusion reactions occur in a high-temperature plasma, the reaction rate per unit volume depends on the particle density n of the reacting fuel particles and on the averaged product 〈σv〉, that is, their mutual reaction cross sections σ times their relative velocity v averaged over the particle velocity distributions. See also: Thermonuclear reaction
For dissimilar reacting nuclei (such as D and T), the reaction rate is given by Eq. (3).
For similar reacting nuclei (for example, D and D), the reaction rate is given by Eq. (4).
Both expressions vary as the square of the total particle density (for a given fuel composition).
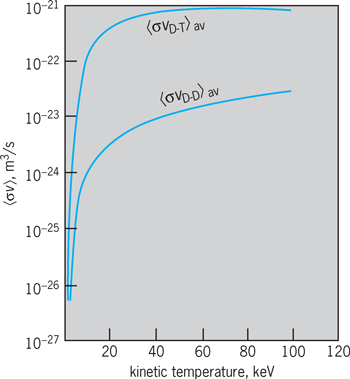
If the particle velocity distributions are known, 〈σv〉 can be determined as a function of energy by numerical integration, using the known reaction cross sections. It is customary to assume a Maxwellian particle velocity distribution, toward which all others tend in equilibrium. The values of 〈σv〉 for the D–D and D–T reactions are shown in Fig. 5. In this plot the kinetic temperature is given in kiloelectronvolts. Just as in the case of the cross sections themselves, the most striking feature of these curves is their extremely rapid falloff with temperature at low temperatures. For example, although at 100 keV for all reactions 〈σv〉 is only weakly dependent on temperature, at 1 keV it varies as T 6.3 and at 0.1 keV as T 133. Also, at the lowest temperatures it can be shown that only the particles in the “tail” of the distribution, which have energies that are large compared with the average, will make appreciable contributions to the reaction rate, the energy dependence of σ being so extreme.
Critical temperatures
The nuclear fusion reaction can obviously be self-sustaining only if the rate of loss of energy from the reacting fuel is not greater than the rate of energy generation by fusion reactions. The simplest consequence of this fact is that there will exist critical, or ideal, ignition temperatures below which a reaction cannot sustain itself, even under idealized conditions. In a fusion reactor, ideal or minimum critical temperatures are determined by the unavoidable escape of radiation from the plasma. A minimum value for the radiation emitted from any plasma is that emitted by a pure hydrogenic plasma in the form of x-rays or bremsstrahlung. Thus plasmas composed only of isotopes of hydrogen and their one-for-one accompanying electrons might be expected to possess the lowest ideal ignition temperatures. This is indeed the case: It can be shown by comparison of the nuclear energy release rates with the radiation losses that the critical temperature for the D–T reaction is about 40 million K. For the D–D reaction it is about 10 times higher. Both radiation rate and nuclear power vary with the square of the particle density, so these critical temperatures are independent of density over the density ranges of interest. The concept of the critical temperature is a highly idealized one, however, because in any real cases additional losses must be expected to occur that will modify the situation, increasing the required temperature.





