Key Concepts
A mechanical wave that can be heard. Sound is a type of mechanical wave that compresses and dilates the fluid or solid medium through which it passes, causing a time-varying perturbation of the local density and pressure within the medium (Fig. 1). The magnitude of perturbations caused by a sound wave are very small, such that there is a linear relationship between the fluctuation in the medium (change in density of a fluid or strain in a solid) and the associated restoring force (pressure gradient). Small-amplitude compressional waves are also called acoustic waves. Other types of mechanical waves are distinguished from sound by the geometry of the perturbation, by the nature of the restoring force, or by highly nonlinear changes in the medium. Examples of mechanical waves that are not considered to be sound include shear waves in solids, bending waves in bars and plates, waves on a string, surface waves, tsunami, and atmospheric waves. See also: Acoustics; Seismology; Wave motion
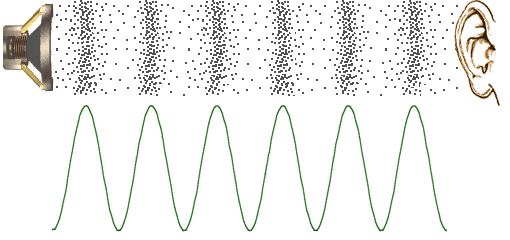
Sound normally reaches our ears by traveling through a fluid medium, such as air or water. Vibrations can also be transmitted via the skull to the inner ear in a process known as bone-conducted sound. Regardless of the transmission path, sound waves must contain frequencies above 20 Hz and below 20 kHz to be audible to a person with normal hearing. Frequencies below 20 Hz are considered infrasound; frequencies above 20 kHz are called ultrasound. See also: Hearing (human); Infrasound
As a sound wave passes by a particular location, the medium at that location oscillates about equilibrium, transmitting the momentum and energy of its motion to neighboring regions of the medium. Thus, the wave is propagated through the medium, while the medium stays essentially in place; it is not carried along with the wave. As a visual example, consider sports fans in a stadium "doing the wave": Individual people do not move far from their seats, though the wave travels around the stadium. Although sound waves are not normally seen, they can be represented by a plot of the acoustic perturbation (usually pressure) as a function of time. Alternatively, sound can be represented by the spatial variation of pressure at a moment in time. Figure 1 depicts the spatially periodic fluctuation of air pressure caused by an oscillating source (a loudspeaker). In this example, the speed of sound in air is constant, so the spatial variation of pressure mimics the temporal variation of pressure at the source. If the motion of the source is sinusoidal, then a plot of pressure versus position along a line connecting the source and receiver will also be sinusoidal. See also: Amplitude (wave motion); Waveform
Sources of sound
All sound is created by a localized disturbance of some medium (usually air or water). The source of the disturbance is typically the motion of a solid object in contact with the medium, but it can also be the unsteady motion of a fluid medium. Both types of sound sources can be heard when riding in a car: Music may be generated from the vibrating surface of a radio loudspeaker, which competes with the noise produced by air flowing in a turbulent way around the car. Sound can also be produced by thermodynamic effects; for instance, localized rapid heating of air causes it to expand quickly, generating a sound pulse. This phenomenon occurs during a lightning strike, creating thunder. On a smaller scale, lasers can also be used to generate sound. See also: Aerodynamic sound; Air; Laser; Loudspeaker; Photoacoustic imaging in biomedicine; Thunder
Both vibrating surfaces and unsteady air flow are types of sources used in musical instruments. A plucked string on a guitar creates a disturbance in the surrounding air, but this vibration acts as a dipole with a source size much smaller than a wavelength, so it does not radiate sound waves efficiently. However, the string transmits its vibrations to the soundboard, which is part of a hollow body. The vibrating soundboard, because it pushes air over a large surface, is a much more efficient radiator of sound. In addition, the air inside the guitar body oscillates with large amplitude at certain frequencies, so it contributes to the overall sound of a guitar. The source of sound in a wind instrument may be the pulses of air that flow through an aperture that opens and closes rapidly, such as a reed or the larynx, or it may result from unsteady flow past an edge, such as in a flute.
For most sounds in air or water, only the frequencies contained in the source vibration are present in the radiated sound. Exceptions to this involve nonlinear sound propagation, which can occur when the amplitude is very large or in certain types of media. See also: Nonlinear acoustics; Sonic boom
If the source oscillates with simple harmonic motion—that is, sinusoidal motion with a single frequency—the resulting sound will be a pure tone of that frequency. A classic example of this motion is the vibration of a simple object connected to a spring that obeys Hooke's law. An extended object, such as a tuning fork, can behave approximately in this way. Another important example of motion that is simply harmonic is the oscillation of air inside a Helmholtz resonator. A bottle is a good example of such a resonator, in which the air in the neck of the bottle moves essentially as a unit, while the air in the larger cavity acts as a spring. See also: Helmholtz resonator; Hooke's law; Tuning fork
Most objects, however, support vibrations of many frequencies, usually due to standing waves. Standing waves in a string or in a column of air occur at frequencies that generally follow the harmonic series. This is why musical instruments that produce a definite pitch utilize strings or tubes of air. Standing waves in thin plates or bars do not occur at harmonic frequencies, primarily because bending waves are dispersive (the speed of sound depends on frequency). See also: Harmonic (periodic phenomena); Mode of vibration
Measurement of sound
The characterization of a sound is based primarily on human perceptual responses. Because of the nature of human perceptions, the correlations between basically subjective evaluations such as loudness, pitch, and timbre, and physical qualities such as energy, frequency, and frequency spectrum, are subtle and not necessarily universal.
Acoustic pressure
An appropriate sensor (such as a microphone or ear) placed in the sound field will detect a time-varying deviation from the equilibrium pressure found at that point within the air. The changing total pressure P measured will vary about the equilibrium pressure P0 by a small amount called the acoustic pressure, . Because the acoustic pressure is fluctuating with time, it is customary to characterize the amplitude of a sound with the peak value or a time-averaged value, such as the root-mean-square pressure prms.
For sound in air, the acoustic pressure is a tiny fraction of atmospheric pressure. Standard atmospheric pressure is approximately 105 Pa, while the acoustic pressure amplitude of a car horn heard 1 m away is approximately 0.1 Pa (one-millionth of atmospheric pressure). Human sensitivity to acoustic pressure ranges from 20 μPa at the frequencies at which the ear is most sensitive to about 20 Pa when the sound is painfully loud. See also: Atmosphere; Microphone; Pressure; Pressure measurement; Sound pressure
Intensity, loudness, and the decibel
The strength of a sound wave is described by its intensity I. From basic physical principles, the instantaneous rate at which energy is transmitted by a sound wave through a unit area is given by the product of acoustic pressure and the component of particle velocity perpendicular to the area. For waves that are spherical or planar (which is approximately true for any wave that is not too close to the source), intensity is proportional to the square of prms. If all quantities are expressed in SI units (pressure amplitude in Pa, speed of sound in m/s, and density in kg/m3), then the intensity will be in watts per square meter (W/m2). See also: Sound intensity
Because of the way the strength of a sound is perceived, it is conventional to specify the intensity of sound in terms of a logarithmic scale, known as sound intensity level (SIL), which has the dimensionless unit of the decibel (dB). To compute the SIL of sound with intensity I, it is necessary to specify a reference intensity Iref. See Eq. (1).
The standard reference level is the threshold of hearing, which is defined as W/m2. This is the smallest sound intensity that can be perceived by an individual with unimpaired hearing for frequencies between 2 and 4 kHz, the frequency range of greatest sensitivity. Thus, the weakest sounds that can be perceived by humans have an intensity level of 0 dB. Normal conversational levels are around 60 dB, and hearing can be damaged if exposed even for short times to levels above 120 dB. See also: Decibel
Every doubling of the intensity increases the intensity level by 3 dB. Because the human perception of loudness is also logarithmic, every successive doubling of the acoustic intensity corresponds to the same incremental increase in loudness. For sounds between about 500 Hz and 4 kHz, the loudness of the sound is doubled if the intensity level increases by roughly 9 dB. Thus, a doubling of loudness corresponds to about an eightfold increase in intensity. For frequencies above 4 kHz or lower than 500 Hz, the sensitivity of the ear is appreciably lessened. Sounds at these frequency extremes must have higher threshold intensity levels before they can be perceived, and an increase in loudness requires a smaller change in the intensity. Thus, the ear behaves rather differently at high loudness levels, where sounds of equal intensities are perceived as similarly loud. It is because of this characteristic that reducing the volume of recorded music causes it to sound thin or tinny, lacking both highs and lows of frequency. See also: Hearing (human); Loudness; Psychoacoustics
Because most sound-measuring equipment detects acoustic pressure rather than intensity, it is convenient to define an equivalent scale in terms of the sound pressure level (SPL). In most applications, the intensity level and sound pressure level are identical, but this is not always true (these levels may not be equivalent for standing waves, for example). For applications that do not involve human perception, sound level is computed using Eq. (1). When the context does involve human exposure to sound (as it often does), the frequency dependence of loudness sensitivity is accounted for using a weighting function. Most commonly used is A-weighting, which is applicable when most of the sound exposure is at levels less than 90 dB. For high sound levels, C-weighting is used, which accounts for the flattening of human loudness response at higher intensities. See also: Acoustic noise
Frequency and pitch
The perception of pitch corresponds to notes on a musical scale. There is a close correspondence between pitch and frequency. Sounds with a higher frequency are perceived as having a higher pitch, with small influences depending on loudness, duration, and the complexity of the waveform. For the pure tones (monofrequency sounds) encountered mainly in the laboratory, pitch and frequency are only approximately proportional. For the more complex waveforms usually encountered, however, the presence of harmonics favors a proportional relationship between pitch and frequency. See also: Pitch
Two tones generated together cannot be distinguished from each other if their frequencies are the same. If their frequencies f1 and (slightly higher) f2 are nearly, but not exactly, identical, the ear will perceive a slow beating, hearing a single tone that is the average of the frequencies of the two individual tones and an amplitude that varies slowly according to the difference between the two frequencies. As f2 increases more, the beating will quicken until it first becomes coarse and unpleasant (dissonant) and then resolves into two separate tones of different pitches. With still further increase, a sense of beating and dissonance will reappear, leading into a blending or consonance that then breaks again into beats and dissonance, and the whole cycle of events repeats. These islands of consonance surrounded by beating and dissonance are attained whenever the ratio of the two frequencies becomes that of small integers, . The larger the integers in the ratio, the subtler the effects become. See also: Beat; Frequency (wave motion)
Frequency spectrum and timbre
Sound waves that consist of a single frequency have a waveform that is sinusoidal and are heard as a "pure tone." As mentioned previously, the sound of a person whistling or blowing across a bottle approximates a pure tone. Most sounds, however, are complex in that they consist of many frequency components, each with a particular amplitude. Component frequencies that are integer multiples of a base, or fundamental, frequency are called harmonics. A sound consisting primarily of harmonics will have a waveform that is periodic with the fundamental frequency and will have a perceived pitch that corresponds to the fundamental. A complex periodic waveform, together with its component harmonics, is illustrated in Fig. 2. Examples of sounds with a definite pitch, consisting of harmonics, include the human voice and those produced by many musical instruments. If the strongest components in a sound are not related harmonically, they are more likely to be perceived individually, and the overall sound will not have a definite pitch. Musicians refer to such frequency components as "overtones" or "partials." Some percussion instruments, such as bells or gongs, produce many discernible overtones when struck. Nonharmonic components that are relatively small in amplitude can contribute a complex character to a sound without interfering with a sense of pitch. Sounds that comprise a broad spectrum of component frequencies, such as footsteps, falling water, or unvoiced consonants, do not have discernible tones. See also: Bell; Harmonic (periodic phenomena)
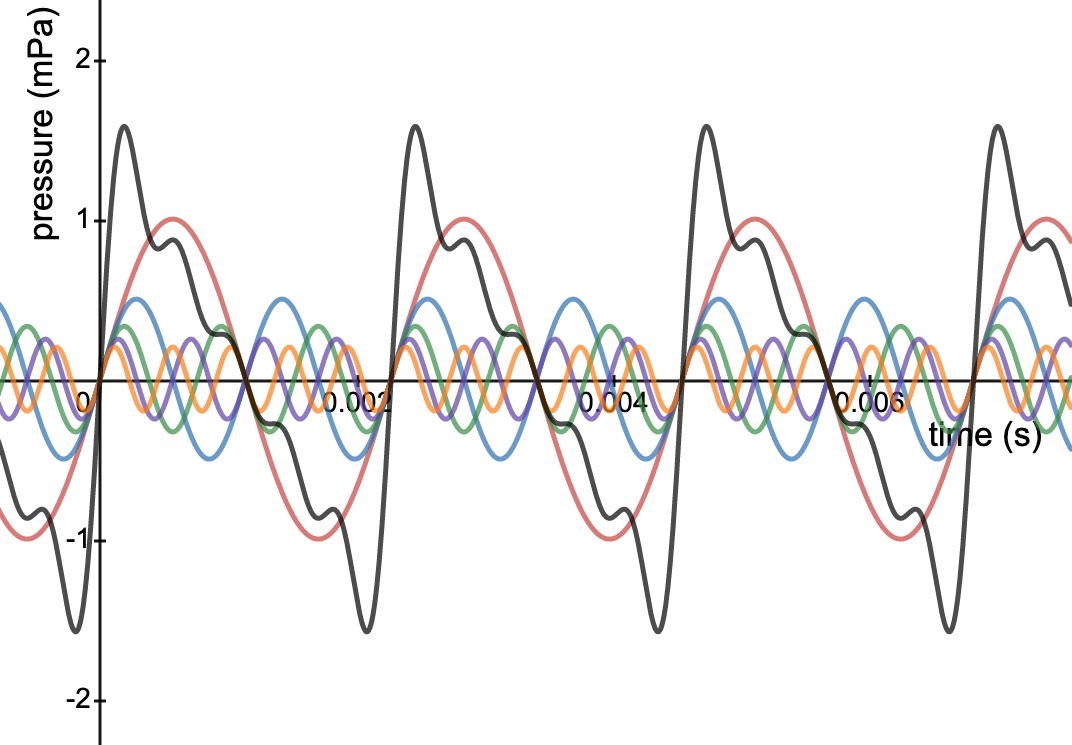
Sounds with a definite pitch, even if they have the same pitch, can be differentiated by the relative amplitudes of the harmonic components. This is perceived as a difference in timbre, which can be characterized by subjective terms such as "bright," "dark," "tinny," or "mellow." The perception of timbre provides a great deal of information about the source of a sound. It enables us to identify musical instruments, different vowel sounds, and even individual speakers. See also: Speech perception
A quantitative representation of the timbre of a sound is the spectrum plot, which shows the amplitude (or intensity) versus frequency of all the components in a sound at a given moment in time. Figure 3 shows the spectrum of the complex waveform in Fig. 2. The technique of analyzing sounds relies on the spectrum plot. Interesting sounds, such as speech and acoustical musical instruments, exhibit time-varying spectra in which the harmonic amplitudes vary with time. Time-variant spectral analysis has many applications, such as automated speech recognition, music recording, animal studies, and noise control.
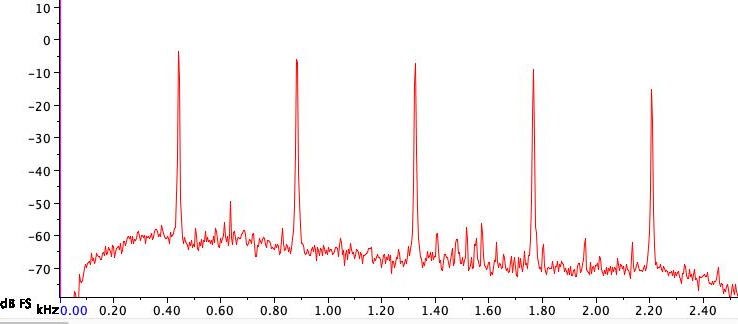
As noted, the relative amplitude of spectral components, and thus the timbre, changes over time. When a chime is struck, many overtones are produced, providing the initial "clang." However, the highest-frequency motions of the bell decay more rapidly than lower ones, leaving a tone with a clear sensation of pitch. Plucking a guitar string near the bridge with a fingernail yields a similar effect. The initial sound of a wind instrument or a bowed string instrument, known as the attack of a note, is indicative of the mechanism by which vibrations are initiated. The brief squeak of the reed in a clarinet, the rasp of a bow on a violin string, or the buzzing of lips on a trumpet is produced before these sources quickly adjust to the natural frequency of the medium. A gong gives a very complex impression throughout its sound because many inharmonic and nonconsonant overtones are present, which die away at different rates, so that the sound seems to shift in pitch and timbre. It is the abundance of harmonics and overtones, the distribution of intensity among them, and how they die away preferentially in time that provide the subjective evaluation of the nature or timbre of the sound. See also: Musical acoustics
Propagation of sound
The sound radiated from a source (such as a loudspeaker, a hand clap, or a voice) must spread outward much like the widening circles from a pebble thrown into a lake. The simplest sound source is one that vibrates uniformly in all directions, like an expanding and contracting bubble. This produces a sound field that is spherically symmetric with an amplitude that decreases with increasing distance from the source, and the fluid elements must have particle velocities that are directed radially. Another source type is the dipole, which corresponds to a sphere moving back and forth in a line. Any object vibrating back and forth that is small compared to the wavelength of the sound it is generating is acting as a dipole. The sound field radiated from a dipole is not the same in all directions: Sound intensity is greatest along the axis of motion, and it is weakest along the axes normal to the motion. More complicated motion of a source, such as expanding along one axis while contracting along another, can be modeled as combinations of dipoles (for example, a quadrupole). See also: Multipole radiation
At distances sufficiently far from any source, the wavefront is nearly planar, in quite the same way that the Earth's surface appears flat to its inhabitants. Plane waves are an important special case of sound because they can be treated as traveling along one dimension, just like waves on a string. For such waves, frequency and wavelength are related simply by the speed of sound, as shown in Eq. (2). The significance of this relationship is that higher frequencies have shorter wavelengths. For sounds in air and water that are not especially loud, the wave speed is constant, so doubling the frequency causes the wavelength to be half as long. This simple inverse relationship enables standing waves to occur at harmonic frequencies.
As a useful reference for estimating wavelengths in air, where c = 343 m/s at 20°C (1125 f/s at 68°F), a sound with a frequency of 1 kHz has a wavelength of 34.5 cm, which is a little longer than a foot. Another feature of plane acoustic waves is that acoustic pressure is in phase with, and directly proportional to, the acoustic particle velocity. The constant of proportionality is the specific acoustic impedance. For plane waves in a fluid, the specific acoustic impedance is the fluid density (ρ) times the speed of sound (c). The relationship between acoustic pressure p and particle velocity v for a plane wave is given by Eq. (3).
Not all sources radiate their sound uniformly in all directions. When someone is speaking in an unconfined space—an open field, for example—a listener circling the speaker hears the voice most well defined when the speaker is facing the listener; the voice loses definition when the speaker is facing away from the listener. Higher frequencies tend to be more pronounced in front of the speaker, whereas lower frequencies are perceived more or less uniformly around the speaker. See also: Acoustic impedance; Diffraction; Wave motion
Speed of sound
The speed of sound in a medium, such as air, is temperature-dependent. For instance, sound moves faster through hot, less dense air than through cold, denser air because the molecules in hot air move faster than in cold air, and thus transmit vibrations more effectively. Expressing this relationship mathematically, acoustic pressure and the density variation are related by Eq. (4),
where the condensation s is and 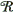 is a constant of proportionality. This is a three-dimensional Hooke's law stating that stress and strain are proportional. The propagation of sound requires such rapid density changes that there is not enough time for thermal energy to flow from compressed (higher-temperature) elements to decompressed (lower-temperature) elements. Because there is little heat flow, the process is nearly adiabatic and
is a constant of proportionality. This is a three-dimensional Hooke's law stating that stress and strain are proportional. The propagation of sound requires such rapid density changes that there is not enough time for thermal energy to flow from compressed (higher-temperature) elements to decompressed (lower-temperature) elements. Because there is little heat flow, the process is nearly adiabatic and 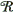 is the adiabatic bulk modulus (rather than the more familiar isothermal modulus relevant to constant-temperature processes). A derivation of the wave equation for a fluid reveals that the speed of sound is given by Eq. (5). Equations (4) and (5) can be combined to give Eq. (6). See also: Adiabatic process
is the adiabatic bulk modulus (rather than the more familiar isothermal modulus relevant to constant-temperature processes). A derivation of the wave equation for a fluid reveals that the speed of sound is given by Eq. (5). Equations (4) and (5) can be combined to give Eq. (6). See also: Adiabatic process
In most fluids, the equation of state is not known, and the speed of sound must be measured directly or inferred from experimental determinations of the bulk modulus. In distilled water, the measured speed of sound in meters per second can be represented by a simplified Eq. (7),
where T is the temperature in degrees Celsius and 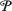 0 is the equilibrium pressure in bars. For most gases at reasonable pressures and temperatures, however, the equation of state is known to be very close to the perfect gas law, so a theoretical expression for the speed of sound in an ideal gas, is Eq. (8).
0 is the equilibrium pressure in bars. For most gases at reasonable pressures and temperatures, however, the equation of state is known to be very close to the perfect gas law, so a theoretical expression for the speed of sound in an ideal gas, is Eq. (8).
Thus, the speed of sound in an ideal gas depends on temperature, increasing as the square root of the absolute temperature. Because many applications of Eq. (8) are for gases around room temperature, it is convenient to re-express the formula in terms of degrees Celsius and the speed of sound c0 at (32°F), as in Eq. (9).
This equation can be used to calculate the speed of sound for a perfect gas at any temperature in terms of the speed of sound in that gas at 0°C (32°F). In air, for example, 331 m/s (1086 ft/s), and at 20°C (68°F) the speed of sound is calculated to be 343 m/s (1125 ft/s). See also: Gas; Heat capacity; Underwater sound
In solids, the sound speed depends on the transverse extent of the solid with respect to the wave. If the solid is rodlike, with transverse dimensions less than the acoustic wavelength, the solid can swell and contract transversely with relative ease, which tends to slow down the wave. For this case, the speed of sound is given by Eq. (10),
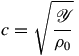 (10)
(10)where 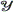 is Young's modulus. If, at the other extreme, the solid has transverse dimensions much larger than the acoustic wavelength, then a longitudinal wave will travel with a greater speed of sound given by Eq. (11),
is Young's modulus. If, at the other extreme, the solid has transverse dimensions much larger than the acoustic wavelength, then a longitudinal wave will travel with a greater speed of sound given by Eq. (11),
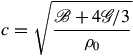 (11)
(11)where 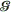 is the shear modulus. These two different propagation speeds are often called bar and bulk sound speeds, respectively. See also: Elasticity; Young's modulus
is the shear modulus. These two different propagation speeds are often called bar and bulk sound speeds, respectively. See also: Elasticity; Young's modulus





