A process that occurs as a result of interactions between atomic nuclei when the interacting particles approach each other to within distances of the order of nuclear dimensions (∼10−12 cm). While nuclear reactions occur in nature, understanding of them and use of them as tools have taken place primarily in the controlled laboratory environment. In the usual experimental situation, nuclear reactions are initiated by bombarding one of the interacting particles, the stationary target nucleus, with nuclear projectiles of some type, and the reaction products and their behaviors are studied. The study of nuclear reactions is the largest area of nuclear and subnuclear (or particle) physics; the threshold for producing pions has historically been taken to be the energy boundary between the two fields.
Types of nuclear interaction
As a generalized nuclear process, consider a collision in which an incident particle strikes a previously stationary particle to produce an unspecified number of final products. If the final products are the same as the two initial particles, the process is called scattering. The scattering is said to be elastic or inelastic, depending on whether some of the kinetic energy of the incident particle is used to raise either of the particles to an excited state. If the product particles are different from the initial pair, the process is referred to as a reaction.
The most common type of nuclear reaction, and the one which has been most extensively studied, involves the production of two final products. Such reactions can be observed, for example, when deuterons with a kinetic energy of a few megaelectronvolts are allowed to strike a carbon nucleus of mass 12. Protons, neutrons, deuterons, and alpha particles are observed to be emitted, and reactions (1)–(4)
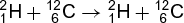 (1)
(1)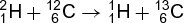 (2)
(2)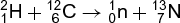 (3)
(3)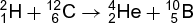 (4)
(4)
are responsible. In these equations the nuclei are indicated by the usual chemical symbols; the subscripts indicate the atomic number (nuclear charge) of the nucleus, and the superscripts the mass number of the particular isotope. These reactions are conventionally written in the compact notation 12C(d,d)12C, 12C(d,p)13C, 12C(d,n)13N, and 12C(d,α)10B, where d represents deuteron, p proton, n neutron, and α alpha particle. In each of these cases the reaction results in the production of an emitted light particle and a heavy residual nucleus. The (d,d) process denotes the elastic scattering as well as the inelastic scattering processes that raise the 12C nucleus to one of its excited states. The other three reactions are examples of nuclear transmutation or disintegration where the residual nuclei may also be formed in their ground states or one of their many excited states. The processes producing the residual nucleus in different excited states are considered to be the different reaction channels of the particular reaction. If the residual nucleus is formed in an excited state, it will subsequently emit this excitation energy in the form of gamma rays or, in special cases, electrons. The residual nucleus may also be a radioactive species, as in the case of 13N formed in the 12C(d,n) reaction. In this case the residual nucleus will undergo further transformation in accordance with its characteristic radioactive decay scheme. See also: Gamma rays; Radioactivity
Nuclear cross section
In general, one is interested in the probability of occurrence of the various reactions as a function of the bombarding energy of the incident particle. The measure of probability for a nuclear reaction is its cross section. Consider a reaction initiated by a beam of particles incident on a region which contains N atoms per unit area (uniformly distributed), and where I particles per second striking the area result in R reactions of a particular type per second. The fraction of the area bombarded which is effective in producing the reaction products is . If this is divided by the number of nuclei per unit area, the effective area or cross section σ = . This is referred to as the total cross section for the specific reaction, since it involves all the occurrences of the reaction. The dimensions are those of an area, and total cross sections are expressed in either square centimeters or barns (1 barn = 10−24 cm2). The differential cross section refers to the probability that a particular reaction product will be observed at a given angle with respect to the beam direction. Its dimensions are those of an area per unit solid angle (for example, barns per steradian).
Requirements for a reaction
Whether a specific reaction occurs and with what cross section it is observed depend upon a number of factors, some of which are not always completely understood. However, there are some necessary conditions which must be fulfilled if a reaction is to proceed.
Coulomb barrier
For a reaction to occur, the two interacting particles must approach each other to within the order of nuclear dimensions (∼10− 12 cm). With the exception of the uncharged neutron, all incident particles must therefore have sufficient kinetic energy to overcome the electrostatic (Coulomb) repulsion produced by the intense electrostatic field of the nuclear charge. The kinetic energy must be comparable to or greater than the so-called Coulomb barrier, whose magnitude is approximately given by the expression ECoul ≈ MeV, where Z and A refer to the nuclear charge and mass number of the interacting particles 1 and 2, respectively. It can be seen that while, for the lightest targets, protons with kinetic energies of a few hundred kiloelectronvolts are sufficient to initiate reactions, energies of many hundreds of megaelectronvolts are required to initiate reactions between heavier nuclei. In order to provide energetic charged particles, to be used as projectiles in reaction studies, particle accelerators of various kinds (such as Van de Graaff generators, cyclotrons, and linear accelerators) have been developed, making possible studies of nuclear reactions induced by projectiles as light as protons and as heavy as 208Pb. See also: Electrostatics; Particle accelerator
Since neutrons are uncharged, they are not repelled by the electrostatic field of the target nucleus, and neutron energies of only a fraction of an electronvolt are sufficient to initiate some reactions. Neutrons for reaction studies can be obtained from nuclear reactors or from various nuclear reactions which produce neutrons as reaction products. There are two other means of producing nuclear reactions which do not fall into the general definition given above. Both electromagnetic radiation and high-energy electrons are capable of disintegrating nuclei under special conditions. However, both interact much less strongly with nuclei than nucleons or other nuclei, through the electromagnetic and weak nuclear forces, respectively, rather than the strong nuclear force responsible for nuclear interactions. See also: Neutron
Q value
For a nuclear reaction to occur, there must be sufficient kinetic energy available to bring about the transmutation of the original nuclear species into the final reaction products. The sum of the kinetic energies of the reaction products may be greater than, equal to, or less than the sum of the kinetic energies before the reaction. The difference in the sums is the Q value for that particular reaction. It can be shown that the Q value is also equal to the difference in the masses (rest energies) of the reaction products and the masses of the initial nuclei. Reactions with a positive Q value are called exoergic or exothermic reactions, while those with a negative Q value are called endoergic or endothermic reactions.
In reactions (1)–(4), where the residual nuclei are formed in their ground states, the Q values are 12C(d,d)12C, Q = 0.0 MeV; 12C(d,p)12C, Q = 2.72 MeV; 12C(d,n)13N, Q = −0.28 MeV; and 12C(d,α)10B, Q = −1.34 MeV. For reactions with a negative Q value, a definite minimum kinetic energy is necessary for the reaction to take place. While there is no threshold energy for reactions with positive Q values, the cross section for the reactions induced by charged particles is very small unless the energies are sufficient to overcome the Coulomb barrier. A nuclear reaction and its inverse are reversible in the sense that the Q values are the same but have the opposite sign [for example, the Q value for the 10B(α,d)12C reaction is +1.39 MeV].
Conservation laws
It has been found experimentally that certain physical quantities must be the same both before and after the reaction. The quantities conserved are electric charge, number of nucleons, energy, linear momentum, angular momentum, and in most cases parity. Except for high-energy reactions involving the production of mesons, the conservation of charge and number of nucleons allow one to infer that the numbers of protons and neutrons are always conserved. The conservation of the number of nucleons indicates that the statistics governing the system are the same before, during, and after the reaction. Fermi-Dirac statistics are obeyed if the total number is odd, and Bose-Einstein if the number is even. The conservation laws taken together serve to strongly restrict the reactions that can take place, and the conservation of angular momentum and parity in particular allow one to establish spins and parities of states excited in various reactions. See also: Angular momentum; Conservation laws (physics); Parity (quantum mechanics); Quantum statistics; Symmetry laws (physics)
Reaction mechanism
What happens when a projectile collides with a target nucleus is a complicated many-body problem which is still not completely understood. Progress made in the last decades has been in the development of various reaction models which have been extremely successful in describing certain classes or types of nuclear reaction processes. In general, all reactions can be classified according to the time scale on which they occur, and the degree to which the kinetic energy of the incident particle is converted into internal excitation of the final products. A large fraction of the reactions observed has properties consistent with those predicted by two reaction mechanisms which represent the extremes in this general classification. These are the mechanisms of compound nucleus formation and direct interaction.
Compound nucleus formation
As originally proposed by N. Bohr, the process is envisioned to take place in two distinct steps. In the first step the incident particle is captured by (or fuses with) the target nucleus, forming an intermediate or compound nucleus which lives a long time (∼10−16 s) compared to the approximately 10−22 s it takes the incident particle to travel past the target. During this time the kinetic energy of the incident particle is shared among all the nucleons, and all memory of the incident particle and target is lost. The compound nucleus is always formed in a highly excited unstable state, is assumed to approach thermodynamic equilibrium involving all or most of the available degrees of freedom, and will decay, as the second step, into different reaction products, or through so-called exit channels. In most cases, the decay can be understood as a statistical evaporation of nucleons or light particles. In the examples of reactions (1)–(4), the compound nucleus formed is 14N, and four possible exit channels are indicated (Fig. 1). In reactions involving heavier targets (for example, A ≈ 200), one of the exit channels may be the fission channel where the compound nucleus splits into two large fragments. See also: Nuclear fission
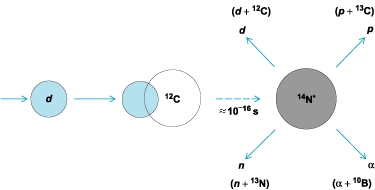
The essential feature of the compound nucleus formation or fusion reaction is that the probability for a specific reaction depends on two independent probabilities: the probability for forming the compound nucleus, and the probability for decaying into that specific exit channel. While certain features of various interactions cannot be completely explained within the framework of the compound nucleus hypothesis, it appears that the mechanism is responsible for a large fraction of reactions occurring in almost all projectile-target interactions. Fusion reactions have been extremely useful in several kinds of spectroscopic studies. Particularly notable have been the resonance studies performed with light particles, such as neutrons, protons, deuterons, and alpha particles, on light target nuclei, and the gamma-ray studies of reactions induced by heavy projectiles, such as 16O and 32S, on target nuclei spanning the periodic table. These studies have provided an enormous amount of information regarding the excitation energies and spins of levels in nuclei. See also: Nuclear spectra
Direct interactions
Some reactions have properties which are in striking conflict with the predictions of the compound nucleus hypothesis. Many of these are consistent with the picture of a mechanism where no long-lived intermediate system is formed, but rather a fast mechanism where the incident particle, or some portion of it, interacts with the surface, or some nucleons on the surface, of the target nucleus. Models for direct processes make use of a concept of a homogeneous lump of nuclear matter with specific modes of excitation, which acts to scatter the incident particle through forces described, in the simplest cases, by an ordinary spherically symmetric potential. In the process of scattering, some of the kinetic energy may be used to excite the target, giving rise to an inelastic process, and nucleons may be exchanged, giving rise to a transfer process. In general, however, direct reactions are assumed to involve only a very small number of the available degrees of freedom.
Most direct reactions are of the transfer type where one or more nucleons are transferred to or from the incident particle as it passes the target, leaving the two final partners either in their ground states or in one of their many excited states. Such transfer reactions are generally referred to as stripping or pick-up reactions, depending on whether the incident particle has lost or acquired nucleons in the reaction. The (d,p) reaction is an example of a stripping reaction, where the incident deuteron is envisioned as being stripped of its neutron as it passes the target nucleus, and the proton continues along its way (Fig. 2).
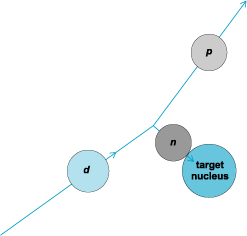
The properties of the target nucleus determine the details of the reaction, fixing the energy and angular momentum with which the neutron must enter it. The energy of the outgoing proton is determined by how much of the deuteron's energy is taken into the target nucleus by the neutron, and indeed serves to identify the final state populated by the Q value of the reaction as a whole. The angular distribution of the differential cross sections will, at appropriate bombarding energies, not be smooth but rather will show a distinct pattern of maxima and minima which are indicative of the spin and parity of the final state. The cross section for populating a specific final state in the target nucleus depends on the nuclear structure of the nuclei involved. This sensitivity has been used in studies of single-nucleon, two-nucleon, and four-nucleon transfer reactions, such as (d,p), (p,d), (3He,d), (t,p), and (7Li,d), to establish the validity and usefulness of the shell-model description of nuclei. Multinucleon transfer reactions with heavier projectiles have been powerful tools for reaching nuclei inaccessible by other means and in producing new isotopes.
Inelastic scattering is also a direct reaction whose angular distribution can provide information about the spin and parity of the excited state. Whereas the states preferentially populated in transfer reactions are those of specific single-particle or shell-model structure, the states preferentially excited in inelastic scattering are collective in nature. The states are most easily understood in the framework of macroscopic descriptions in which they are considered to be oscillations in shape about a spherical mean (vibrations) or to be the rotations of a statically deformed shape. The cross section for inelastic scattering is related to the shape or deformation of the target nucleus in its various collective excitations. Inelastic excitation can be caused by both a nuclear interaction and an electromagnetic interaction known as Coulomb excitation, where the target nucleus interacts with the rapidly changing electric field caused by the passage of the charged particle. Coulomb excitation is an important process at low bombarding energies in interactions involving heavy projectiles. Studies in inelastic scattering to low-lying states of nuclei across the periodic table have provided graphic demonstrations of the collective aspects of nuclei. See also: Coulomb excitation
Elastic scattering is the direct interaction which leaves the interacting particles unchanged. For charged particles at low bombarding energies, the elastic scattering is well described in terms of the inverse-square force law between two electrically charged bodies. In this case, the process is known as Rutherford scattering. At higher energies the particles come into the range of the nuclear force, and the elastic scattering deviates from the inverse-square behavior. See also: Nuclear structure; Scattering experiments (nuclei)
More complex reaction mechanisms
Processes intermediate between direct and compound nucleus formation do occur. The best example of such a process is the so-called preequilibrium emission, where light particles are emitted before the kinetic energy has been shared among all the nucleons in the compound nucleus. Another example is seen in the interaction of two massive nuclei, such as 84Kr + 209Bi, where the probability for formation of the compound nucleus is found to be very small. The experimental observations indicate that the nuclei interact for a short time and then separate in what appears to be a direct reaction. Although the interaction times for these so-called strongly damped or deep inelastic collisions are very small compared to that for compound nucleus formations, they are sufficiently long for considerable mass transfer and loss of relative kinetic energy to occur.
Nuclear reaction studies
In most instances the study of nuclear reactions is directed toward the long-range goal of obtaining information about the properties and structure of nuclei. Such studies usually proceed in two stages. In the first stage the attention focuses on the mechanism of the reaction and on establishing the dependence on the nuclei involved. The specific models proposed continue to be modified and improved, as they are confronted with more experimental results, until their predictions become reliable. At that point the second stage is entered, in which the focus of the effort is on extraction of information about nuclei.
There are other studies which are focused on reaction cross-section behaviors for other purposes. Examples of this are the neutron-capture reactions on heavy target nuclei that fission, and the 3H(d,n)4He reaction, important in thermonuclear processes, which continue to be studied because of their application as energy sources. Studies of the interactions of light nuclei at low energies are intensely studied because of their implications for astrophysics and cosmology. See also: Nuclear fusion; Nucleosynthesis; Thermonuclear reaction
Collisions of very high energy nuclei
The protons and neutrons which make up nuclei are not elementary particles. They are each clusters of quarks, tightly bound together by the exchange of gluons. One central characteristic of quantum chromodynamics, the theory which describes the interactions of quarks and gluons, is that the force between quarks becomes weaker as the quarks interact at higher energies. During most nuclear reactions, the force between quarks is so strong that free quarks cannot exist; quarks only occur confined in composite particles called hadrons. Protons and neutrons are hadrons, and there are many other types, such as pions and J/ψ particles, which are unstable. However, at temperatures above a critical temperature value of about 150 MeV (about 1012 K, or about 105 times the temperature at the center of the Sun), quantum chromodynamics predicts that the force between the quarks will be so weakened that hadrons will fall apart. The transition between hadronic matter and a plasma of quarks and gluons is called the quantum chromodynamics phase transition.
For the first few microseconds after the big bang, the whole universe was hotter than 150 MeV and was filled with quark-gluon plasma. The quantum chromodynamics phase transition occurred throughout the universe as it cooled through the critical temperature. The extreme temperatures required to observe the quantum chromodynamics phase transition are difficult to obtain in a laboratory. The only method known is to collide large nuclei at very high energies. See also: Big bang theory; Particle accelerator
Detailed theoretical calculations which simulate the quantum chromodynamics interactions of the thousands of quarks and gluons produced in such collisions lend support to the expectation that under these conditions quark-gluon plasma will be created for the first time since the big bang. This plasma will occur in a region several times 10−13 cm in size, and will exist for several times 10−22 s before the quantum chromodynamics phase transition occurs and ordinary hadrons are reformed.
The distribution and energy of the particles emerging from the collision should carry signatures of the fleeting presence of a quark-gluon plasma. One such signature involves the J/ψ particle, which is made of a heavy quark and a heavy antiquark. In a quark-gluon plasma, the J/ψ (like any hadron) dissociates and the heavy quark and antiquark separate. When the plasma cools through the phase transition, heavy quarks are much more likely to form hadrons in combination with the far more numerous light quarks than to reunite to form J/ψ hadrons. The expected reduction in the number of J/ψ particles produced in a collision has in fact been detected. However, J/ψ hadrons can also be broken apart by repeated collisions in a hot, dense hadronic environment. Therefore, the observed J/ψ suppression establishes that such an environment has been created, but does not in itself demonstrate the creation of a quark-gluon plasma. See also: J/psi particle
In an idealized model, as the hadronic state of matter is reestablished after an abrupt quantum chromodynamics phase transition, pion waves are amplified and coherent emission of pions occurs. Such pion lasers would be easily observable, because they would occasionally emit only electrically neutral pions or only electrically charged ones, whereas ordinarily different types of pions are uniformly mixed. This effect would be an unambiguous signature for the brief presence of a quark-gluon plasma in a collision of very high energy nuclei. See also: Gluons; Phase transitions; Quantum chromodynamics; Quark-gluon plasma; Quarks; Relativistic heavy-ion collisions





