First law

Kepler's first law states that a planet moves in an elliptical orbit around the Sun, which is located at one of the two foci of the ellipse.

An ellipse is a conic curve, usually defined algebraically and ranges from a circle (formed when a plane cuts the cone perpendicularly to its axis) up to a parabola (formed by the intersection of a cutting plane parallel to the side of the cone). As the plane approaches perpendicularity with the axis, the ellipse approaches a circle; Kepler's first law accepts a circular orbit as the limiting case of an ellipse. As the cutting plane approaches a position parallel to the side of the cone, the ellipse approaches a parabola; although a body can move in a parabolic path around another placed at its focus, it would not be a planet in the accepted sense because it would never return. An ellipse is also defined as the locus of points the sum of whose distances from two fixed points (the foci) is a constant. See also: Circle; Conic section; Ellipse

Kepler discovered the first law by analyzing the observations that Danish astronomer Tycho Brahe had made of the planet Mars in the late sixteenth century. An earlier astronomer of that century, the Polish doctor and astronomer Nicolaus Copernicus, had broken with the common-sense notion, apparently supported by daily experience, that the Earth is the center of the universe around which all other bodies move. Instead, Copernicus proposed a heliocentric theory, in which the Sun is at the center. Copernicus had, however, accepted another tradition in astronomy, that all heavenly appearances are to be explained by combinations of circles, which were held to be perfect figures. Kepler's ellipses shattered that tradition. The ellipses also challenged another premise of earlier astronomy, that the heavens are fundamentally different from the Earth. Although Kepler discovered the ellipse by studying Mars, he generalized the shape to the orbits of all the planets, including Earth. See also: Earth; Mars

In 1610, the year after Kepler published his first law, the Italian physicist and astronomer Galileo discovered the satellites of Jupiter and later in the seventeenth century satellites were observed around Saturn. All of these bodies obey Kepler's first law. In 1687, Newton demonstrated that any body, moving in an orbit around another body that attracts it with a force that varies inversely as the square of the distance between them, must move in a conic section. This path will be an ellipse when the velocity is below a certain limit in relation to the attracting force. Thus the first law is not limited to primary planets around the Sun or to heavenly bodies. It is a general law that applies to all satellites held in orbit by an inverse-square force. See also: Force; Jupiter; Saturn

Second law

Kepler's second law states that the radius vector of an ellipse (the imaginary line between the planet and the Sun) sweeps out equal areas in equal times (see Fig. 2).

Fig. 2 Demonstration of Kepler's first and second laws. The planet moves along an elliptical orbit at a nonuniform rate, so that the radius vector drawn to the Sun, which is located at one focus of the ellipse, sweeps out areas that are proportional to time. Thus, the planet will take equal times (corresponding to the equal areas) to traverse the unequal distances along the ellipse that correspond to the two shaded areas. The diagram greatly exaggerates the eccentricity of any orbital ellipse in the solar system.

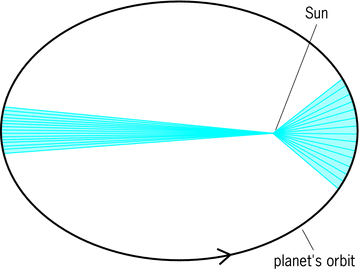
Astronomers needed to predict the location of planets at given times. The conventional system in Kepler's time, of combining circles that were assumed to turn uniformly, had made it possible to calculate an approximate position at any time by the vectorial addition of the radii. In rejecting the system of circles, Kepler sought some other method by which to predict locations to within the accuracy of Brahe's observations of Mars, and this Kepler provided with his second law. A planet does not move along its elliptical path at a uniform velocity; it moves more swiftly when it is closer to the Sun and more slowly when it is farther removed. Behind the nonuniform velocities, the second law finds a uniformity in the areas described in equal time intervals. See also: Velocity

Again, Newton demonstrated the dynamic cause behind Kepler's second law. In this case, it is not restricted to forces that vary inversely as the square of the distance; rather, it is valid for all forces of attraction between the two bodies, regardless of the law the forces obey. The second law expresses the principle of the conservation of angular momentum. If body B moves in relation to body A in a straight line with a uniform velocity, it has a constant angular momentum in relation to A and the line joining B to A sweeps out equal areas in equal increments of time. No force of attraction (or repulsion) between the two bodies can alter their angular momentum about each other. The second law thus expresses a relation that holds for all pairs of bodies with radial forces between them. See also: Angular momentum

Third law

Kepler's third law states that there is a constant ratio between the square of the orbital period of a planet to the cube of the planet's semimajor axis. The orbital period is the time required for a planet to complete one orbit, while the semimajor axis is half the length of the long axis of the ellipse, a value that is approximately equal to the mean radius, which is the average distance from the Sun during one orbit.

Kepler's first two laws govern the orbits of individual planets around the Sun. His third law defines the relative scale of the system of planets. The four satellites that Galileo had discovered around Jupiter were found to obey the third law, as did the satellites later found around Saturn. Newton demonstrated once again that the third law is valid for every system of satellites around a central body that attracts them, as the Sun attracts the planets, with a force that varies inversely as the square of the distance.

Kepler's three laws of planetary motion are all premised on the phenomenon, proved by Kepler himself, that the planes of the planetary orbits all pass through the Sun (some have referred to this discovery as Kepler's zeroth law).

Significance and limitations

Kepler's laws revolutionized astronomy in their recognition of the value of high-precision observation and by improving the prediction of planetary positions by a factor of 20. With the aid of his laws, Kepler was able to predict with full confidence transits of Mercury and Venus in 1631. The Venus transit was not witnessed in Europe, even though modern calculations have shown that it should have been visible from Italy and farther eastward. The French philosopher, physicist, and priest, Pierre Gassendi witnessed the Mercury transit in Paris “a little earlier than was expected” on November 7. No theory of planetary motion based on circular motion (including Copernicus's) could have made such a prediction.

Kepler was strongly motivated by physical reasoning to seek the causes of observed planetary motion, but his derivation of the three laws was based strictly on geometric arguments constrained by the unprecedentedly accurate observations of Tycho. Because the laws are purely kinematically derived, they do not precisely describe the motions of the planets around the Sun, for the real motions involve forces that act not only between the Sun and individual planets but also, in accordance with Newton's law of universal gravitation, mutually among all the planets. In the case of the Moon orbiting the Earth, the attraction that the Sun exerts on the Moon is large enough to introduce perturbations, which astronomers had identified empirically before Kepler stated his three laws. Because the Sun is immensely more massive than the planets, the perturbations caused by the planets' mutual attractions are quite small and Kepler's laws offer an accurate first approximation of their motions. Kepler's laws of planetary motion were the first of the mathematical laws of modern science; they did much to determine the pattern that science has continued to pursue. See also: Celestial mechanics; Gravity; Orbital motion; Perturbation (astronomy)

Terence J. Mahoney