Key Concepts
A phenomenon resulting from an instability of the atomic nucleus in certain atoms whereby the nucleus experiences a spontaneous but measurably delayed nuclear transition or transformation with the resulting emission of radiation. The most commonly found types of radioactivity are alpha (Fig. 1), beta negatron, beta positron, electron capture, and isomeric transition. Each is characterized by the particular type of nuclear radiation which is emitted by the transforming parent nucleus. In addition, there are several other decay modes that are observed more rarely in specific regions of the periodic table (Table 1). Several of these rarer processes are in fact two-step processes. See also: Alpha particles; Beta particles; Periodic table; Radiation
| Type | Symbol | Particles emitted | Change in atomic number, Δ Z | Change in atomic mass number, Δ A | Example |
|---|---|---|---|---|---|
| Alpha | α | Helium nucleus | −2 | −4 | 22686Ra → 22284Rn + α |
| Beta negatron | β− | Negative electron and antineutrinoa | +1 | 0 | 2411Na → 2412Mg + e- + v |
| Beta positron | β+ | Positive electron and neutrinoa | −1 | 0 | 2211Na → 2210Ne + e+ + v |
| Electron capture | EC | Neutrino | −1 | 0 | 74Be + e- → 73Li + v |
| Isomeric transitionb | IT | Gamma rays or conversion electrons or both (and positive-negative electron pair)c | 0 | 0 | 137m56Ba → 13756Ba + γ or conversion electrons |
| Proton | p | Proton | −1 | −1 | 15171La → 15070Yb + p |
| Spontaneous fission (hot) | SF | Two intermediate-mass nuclei and 1–10 neutrons | Various | Various | 23892U → 13350Sn + 10342Mo + 2n |
| Spontaneous fission (cold) | SF | Two intermediate-mass nuclei (zero neutrons) | Various | Various | 25298Cf → 10642Mo + 14656Ba |
| Ternary spontaneous fission (hot) | TSF | Two intermediate-mass nuclei, a light particle (2H, α, up to 10Be), and neutrons | Various | Various | 25298Cf → 10040Zr + 14656Ba + α + 2n |
| Ternary spontaneous fission (cold) | TSF | Two intermediate-mass nuclei and a light particle | Various | Various | 25298Cf → 9638Sr + 14656Ba + 104Be |
| Isomeric spontaneous fission | ISF | Heavy fragments and neutrons | Various | Various | 244f95Am → 13453I + 10742Mo + 3n |
| Beta-delayed spontaneous fission | (EC + β+) SF | Positive electron, neutrino, heavy fragments, and neutrons | Various | Various | 24699Es → β+ + v + 246f98Cf → 13854Xe + 10744Ur + n |
| β- SF | Negative electron, antineutrino, heavy fragments, and neutrons | Various | Various | 23691Pa → β- + v + 236f92U → 13953I + 9739Y + 3n | |
| Beta-delayed neutron | β- n | Negative electron, and antineutrino, neutron | +1 | -1 | 113Li → β- + v + 114Be* → 104Be + n |
| Beta-delayed two-neutron (three-, four-neutron) | β- 2n(3n, 4n) | Negative electron, antineutrino, and two (three, four) neutrons | +1 | -2 (-3, -4) | 113Li → β- + v + 114Be* → 9(8)4Be + 2n(3n) |
| Beta-delayed proton | β+ p or (β+ + EC)p | Positive electron, neutrino, and proton | -2 | -1 | 11455Cs → β+ + v + 11454Xe* → 11353I + p |
| Beta-delayed two-proton | β+ 2p | Positive electron, neutrino, and two protons | -3 | -2 | 2213Al → β+ + v + 2212Mg*- → 2010Ne + 2p |
| Beta-delayed triton | β- 31H | Negative electron, antineutrino, and triton | 0 | -3 | 113Li → β- + v + 114B* → 83Li + 31H |
| Beta-delayed alpha | β+ α | Positive electron, neutrino, and alpha | -3 | -4 | 11455Cs → β+ + v + 11454Xe* → 11052Te + α |
| β- α | Negative electron, antineutrino, and alpha | -1 | -4 | 21483Bi → β- + v + 11484Po* → 21082Pb + α | |
| Beta-delayed alpha-neutron | β- α, n | Negative electron, antineutrino, alpha, and neutron | -1 | -5 | 113Li → β- + v + 114B* → 62He + α + n |
| Double beta decay | β- β- | Two negative electrons and two antineutrinos | +2 | 0 | 8234Se → 8236Kr + 2β- + 2v |
| β+ β+ | Two positive electrons and two neutrinos | -2 | 0 | d13056Ba → 13054Xe + 2β+ + 2v | |
| Double electron captured | EC EC | Two neutrinos | -2 | 0 | d13056Ba + 2e- → 13054Xe + 2v |
| Neutrinoless double beta decaye | β- β- | Two negative electrons | +2 | 0 | e9234Se → 8236Kr + 2β- |
| Two-proton | 2p | Two protons | -2 | -2 | 45Fe → 43Cr + 2p |
| Neutrond | n | Neutron | 0 | -1 | |
| Two-neutrond | 2n | Two neutrons | 0 | -2 | |
| Heavy clustersff | 146C | 146C nucleus | -6 | -14 | 22388Ra → 20982Pb + 146C |
| 208O | 146O nucleus | -8 | -20 | 22789Ac → 20781Tl + 208O | |
| 2410Ne | 2410Ne nucleus | -10 | -24 | 23292U → 20882Pb + 2410Ne |
a The neutrinos and antineutrinos emitted in beta decay are electron neutrinos and antineutrinos.
b Excited states with relatively long measured half-lives are called isomeric and are identified by placing the symbol m for metastable after the mass number, as in 137mBa. Excited states with essentially prompt decay are identified by asterisks, as in 11Be*.
c Pair emission occurs as an additional competing decay mode when the decay energy exceeds 1.022 MeV.
d Theoretically predicted but not definitively established experimentally.
e Theoretically possible and predicted in some grand unified theories.
f There are other possible clusters in addition to those shown. Cold SF is also a type of cluster radioactivity.
A particular radioactive transition may be delayed by less than a microsecond or by more than a billion years, but the existence of a measurable delay or lifetime distinguishes a radioactive nuclear transition from a so-called prompt nuclear transition, such as is involved in the emission of most gamma rays. The delay is expressed quantitatively by the radioactive decay constant, or by the mean life, or by the half-period (also called half-life) for each type of radioactive atom. See also: Gamma ray; Half-life
History of discovery
The discovery of radioactivity by French physicist Henri Becquerel in 1896 was an indirect consequence of the discovery of x-rays a few months earlier by German physicist Wilhelm Röntgen, and marked the birth of nuclear physics. On the other hand, nuclear physics can also be said to begin with the proposal by New Zealand-born British physicist Ernest Rutherford in 1911 that atoms have a nucleus. On the basis of the scattering of alpha particles (emitted in radioactive decay) by gold foils, Rutherford proposed a solar model of atoms, where negatively charged electrons orbit the tiny nucleus, which contains all the positive charge and essentially all the mass of the atom, as planets orbit around the Sun. The attractive Coulomb electrical force holds the electrons in orbit about the nucleus. Atoms have radii of about 10−10 m and the nuclei of atoms have radii about 2 × 10−15 m, so atoms are mostly empty space, like the solar system. Danish physicist Niels Bohr proposed a theoretical model for the atom that removed certain difficulties of the Rutherford model. See also: Atom; Atomic nucleus; Atomic structure and spectra; Electric charge; Nuclear physics; X-ray
However, it was only after the discovery of the neutron in 1932 that a proper understanding was achieved of the particles that compose the nucleus of the atom. The nucleus contains protons that carry positive charge and neutrons with slightly higher mass and zero net electrical charge. These protons and neutrons (called nucleons) are held inside the nucleus by the nuclear force between these particles. This force gives rise to the binding energy of the nucleus, which is the energy required to pull all the protons and neutrons apart. The binding energy makes the mass of a nucleus less than the masses of the Z protons and N neutrons that make up the nucleus. In all radioactive decays the total number of nucleons, A = Z + N, before and after the decay is a constant; that is, the number of nucleons is conserved. Differences in binding energies produce differences in masses which in turn determine what type of radioactive decay can occur. Radioactive decay occurs when the masses of all the particles after the decay are less than the mass of the original radioactive nucleus. See also: Neutron; Nuclear binding energy; Nuclear structure; Nucleon; Proton
In 1934, the French chemists Irène Joliet-Curie and Frédéric Joliot demonstrated that radioactive nuclei can be made in the laboratory. All chemical elements may be rendered radioactive by adding or by subtracting (except for hydrogen and helium) neutrons from the nucleus of the stable ones. Studies of the radioactive decays of new isotopes far from the stable ones in nature continue as a major frontier in nuclear research. The availability of this wide variety of radioactive isotopes has stimulated their use in many different fields, including chemistry, biology, medicine, industry, artifact dating, agriculture, and space exploration. See also: Isotope; Radioactivity and radiation applications
Transition rates and decay laws
This section covers radioactive decay constant, dual decay, exponential decay law, mean life, and half-period.
Radioactive decay constant
The rate of radioactive transformation, or the activity, of a source equals the number A of identical radioactive atoms present in the source, multiplied by their characteristic radioactive decay constant λ. Thus Eq. (1) holds,
where the decay constant λ has dimensions of s−1. The numerical value of λ expresses the statistical probability of decay of each radioactive atom in a group of identical atoms, per time. For example, if λ = 0.01 s−1 for a particular radioactive species, then each atom has a chance of 0.01 (1%) of decaying in 1 s, and a chance of 0.99 (99%) of not decaying in any given 1-s interval. The constant λ is one of the most important characteristics of each radioactive nuclide: λ is essentially independent of all physical and chemical conditions such as temperature, pressure, concentration, chemical combination, or age of the radioactive atoms. There are a few cases where very small measurable effects are observed for different chemical combinations and pressure. However, in the Sun and in space a nucleus may be stripped of its atomic electrons, and then electron capture decay rates can change markedly; for example, the half-life of 7Be is 70 d in the Sun and 53 d on Earth, and the half-life of 54Mn is estimated to be (1–2) × 106 y in cosmic rays compared to 312 d on Earth because on average they have essentially no orbital electrons for electron captures to occur.
The identification of some radioactive samples can be made simply by measuring λ, which then serves as an equivalent of qualitative chemical analysis. For the most common radioactive nuclides, the range of λ extends from 3 × 106 s−1 (for thorium C′) to 1.6 × 10−18 s−1 (for thorium).
Dual decay
Many radioactive nuclides have two or more independent and alternative modes of decay. For example, 238U can decay either by alpha-particle emission or by spontaneous fission. A single atom of 64Cu can decay in any of three competing independent ways: negatron beta-particle emission, positron beta-particle emission, or electron capture. When two or more independent modes of decay are possible, the nuclide is said to exhibit dual decay.
The competing modes of decay of any nuclide have independent partial decay constants given by the probabilities λ1, λ2, λ3 … per second, and the total probability of decay is represented by the total decay constant λ, defined by Eq. (2).
If there are A identical atoms present, the partial activities, as measured by the different modes of decay, are Aλ1, Aλ2, Aλ3, …, and the total activity Aλ is given by Eq. (3).
The partial activities, Aλ1, …, such as positron beta particles from 64Cu, are proportional to the total activity, Aλ, at all times.
The branching ratio is the fraction of the decaying atoms which follow a particular mode of decay, and equals Aλ1/Aλ or λ1/λ. For example, in the case of 64Cu the measured branching ratios are λ1/λ = 0.40 for negatron beta decay, λ2/λ = 0.20 for positron beta decay, and λ3/λ = 0.40 for electron capture. The sum of all the branching ratios for a particular nuclide is unity.
Exponential decay law
The total activity, Aλ, equals the rate of decrease −dA/dt in the number of radioactive atoms A present. Because λ is independent of the age t of an atom, integration of the differential equation of radioactive decay, −dA/dt = Aλ, gives Eq. (4),
where ln represents the natural logarithm to the base e, and A atoms remain at time t if there were A0 atoms initially present at time t0. If t0 = 0, then Eq. (4) can be rewritten as the exponential law of radioactive decay in its most common form, Eq. (5).
The initial activity at t = 0 was A0λ, and the activity at t, when only A atoms remain untransformed, is Aλ. Because λ is a constant, the fractional activity Aλ/A0λ at time t and the fractional amount of radioactive atoms A A0 are given by Eq. (6).
In cases of dual decay, the partial activities Aλ1, Aλ2, … also decrease with time as e− λ t1, not as e− λ t1…, because Aλ1/A0λ1 = A/A0 = e−λ t where λ is the total decay constant. This is because the decrease of each partial activity with time is due to the depletion of the total stock of atoms A, and this depletion is accomplished by the combined action of all the competing modes of decay.
Mean life
The actual life of any particular atom can have any value between zero and infinity. The average or mean life of a large number of identical radioactive atoms is, however, a definite and important quantity.
If there are A0 atoms present initially at t = 0, then the number remaining undecayed at a later time t is A = A0e− λt, by Eq. (5). Each of these A atoms has a life longer than t. In an additional infinitesimally short time interval dt, between time t and t + dt, the absolute number of atoms which will decay on the average is Aλdt, and these atoms had a life-span t. The total L of the life-spans of all the A0 atoms is the sum or integral of tAλ dt from t = 0 to t = ∞, which is given by Eq. (7).
Then the average lifetime L/A0, which is called the mean life τ, is given by Eq. (8),
where λ is the total radioactive decay constant of Eq. (2).
Substitution of t = τ = 1/λ into Eq. (6) shows that the mean life is the time required for the number of atoms, or their activity, to fall to e−1 = 0.368 of any initial value.
Half-period (half-life)
The time interval over which the chance of survival of a particular radioactive atom is exactly one-half is called the half-period T (also called half-life, written T1/2. From Eq. (4), Eq. (9) is obtained.
Then the half-period T is related to the total radioactive decay constant λ, and to the mean life τ, by Eq. (10).
For mnemonic reasons, the half-period T is much more frequently employed than the total decay constant λ or the mean life τ. For example, it is more common to speak of 232Th as having a half-period of 1.4 × 1010 years than to speak of its mean life of 2.0 × 1010 years or its total decay constant of 1.6 × 10−18 s−1, although all three are equivalent statements of the average longevity of 232Th atoms.
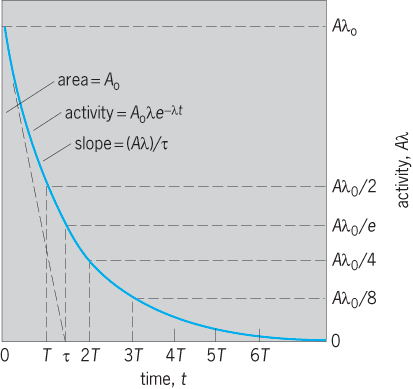
Any initial activity A0λ is reduced to ½ in one half-period T, to 1/e in one mean life τ, to ¼ in two half-periods 2T, and so on (Fig. 2). The slope of the activity curve, or rate of decrease of activity, is d(Aλ)/dt = λdA/dt = −λ(Aλ). Thus the initial slope is −λ(A0λ) = −(A0λ)/τ. The area under the activity curve, if integrated to t = ∞, is simply A0, the total initial number of radioactive atoms. Also, the initial activity A0λ, if it could continue at a constant value for one mean life τ, would exactly destroy all the atoms because (A0λ)τ = A0. See also: Half-life
Radioactive series decay
In a number of cases, a radioactive nuclide A decays into a nuclide B that is also radioactive; the nuclide B then decays into C which is also radioactive, and so on. For example, 23290Th decays into a series of 10 successive radioactive nuclides. Substantially all the primary products of nuclear fission are negatron beta-particle emitters which decay through a chain or series of two to six successive beta-particle emitters before a stable nuclide is reached as an end product. See also: Nuclear fission
Let the initial part of such a series be represented by reaction (11),
where radioactive atoms of types A, B, C, D, … have radioactive decay constants given by λA, λB, λC, λD, … . Then if there are initially present, at time t = 0, A0 atoms of type A, the numbers A, B, C, … of atoms of types A, B, C, … , which will be present at a later time t, are given by Eqs. (12)–(14),
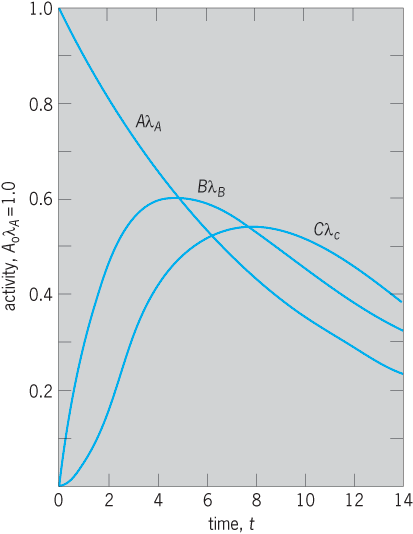
and the activities of A, B, C, … are AλA, BλB, CλC, … (Fig. 3). General equations describing the amounts and activities of any number of radioactive decay products are more complicated and are given in standard texts.
Radioactive equilibrium
In Fig. 4, the ratio BλB/AλA of the activities of the parent A and the daughter product B change with time. The activity BλB is zero initially and also after a very long time, when all the atoms have decayed. Thus BλB passes through a maximum value, and it can be shown that this occurs at a time tm given by Eq. (15).
The situation in which the activities AλA and BλB are exactly equal to each other is called ideal equilibrium, and exists only at the moment tm .
If the parent A is longer-lived than the daughter B, as occurs in many cases, then at a time which is long compared with the mean life τB of B, the activity ratio approaches a constant value given by Eq. (16),
where TA and TB are the half-periods of A and of B. When the activity ratio BλB/AλA is constant, a particular type of radioactive equilibrium exists. This is spoken of as secular equilibrium if the activity ratio is experimentally indistinguishable from unity, as occurs when TA is very much greater than TB .
Equilibrium concepts are applied also between a long-lived parent and any of its decay products in a long series. For example, in a sufficiently old uranium ore, radium (T = 1620 years) is in secular equilibrium with its ultimate parent uranium (T = 4.5 × 109 years) although there are four intermediate radioactive substances intervening in the series between uranium and radium. Here, secular equilibrium shows that activities of radium and uranium continue to be equal to each other even though the activity of the parent uranium is decreasing with time.
When TB is comparable with TA, Eq. (16) shows that the equilibrium ratio will clearly exceed unity; this situation is spoken of as transient equilibrium. For example, in fission-product decay series (17)
the half-period of 140Ba is 307 h and that of 140La is 40 h. In an initially pure source of 140Ba the activity of 140La starts at zero, rises to a maximum at tm = 135 h [Eq. (15)], then decreases, and after a few hundred hours is in transient equilibrium with its parent, when the 140La activity [by Eq. (16)] is 307/(307 – 40) = 1.15 times the activity of its parent 140Ba.
Radioactivity in the Earth
A number of isotopes of elements found in the Earth are radioactive (Table 2). All known or theoretically predicted isotopes of elements above lead are radioactive. As a general rule, one can detect the presence of a radioactive substance for about 10 half-lives. Therefore, activities with T ≲ 0.3 × 109 years should not be found in the Earth. For example, present-day uranium is an isotopic mixture containing 99.3% 238U, whose half-period is 4.5 × 109 years, and only 0.7% of the shorter-lived uranium isotope 235U, whose half-period is 0.7 × 109 years, whereas these isotopes presumably were produced in roughly equal amounts in the Earth a few billion years ago. Geophysical evidence indicates that originally some 236U was present also, but none is found in nature now as expected with its half-period of 0.02 × 109 years. The elements technetium (Z = 43) and promethium (Z = 61) are not found in the Earth's crust because all their isotopes are radioactive with much shorter half-periods (their longest-lived are T = 2.6 × 106 years for 97Tc and T = 17.7 years for 145Pm).
| Nuclide | |||||
|---|---|---|---|---|---|
| Atomic number, Z | Mass number, Z | Percent abundance in nature | Half-period, years | Radioactive transitions observeda | Decay energy, MeVa |
| 19 K | 40 | 0.0117 | 1.3 × 109 | β-, EC | β- 1.3 – EC 1.5 |
| 34 Se | 82 | 8.73 | 0.92 × 1020 | β- β- | 3.0 |
| 37 Rb | 87 | 27.83 | 4.97 × 1010 | β- | 0.3 |
| 48 Cd | 113 | 12.2 | 7.7 × 1015 | β- | 0.3 |
| 49 In | 115 | 95.71 | 4.4 × 1014 | β- | 0.5 |
| 52 Te | 130 | 34.08 | 2 × 1021 | Growth of 13054XEb | 1.6 |
| 57 La | 138 | 0.090 | 1.0 × 1011 | β-, EC | β- 1.0 – EC 1.75 |
| 60 Nd | 144 | 23.8 | 2.3 × 1015 | α | 1.9 |
| 62 Sm | 147 | 14.99 | 1.1 × 1011 | α | 2.3 |
| 62 Sm | 148 | 11.24 | 7 × 1015 | α | 1.99 |
| 64 Gd | 152 | 0.20 | 1.1 × 1014 | α | 2.2 |
| 71 Lu | 176 | 2.59 | 3.76 × 1010 | β-, γ | 0.6 |
| 72 Hf | 174 | 0.16 | 2 × 1015 | α | 2.5 |
| 75 Re | 187 | 62.6 | 4.1 × 1010 | β- | 0.003 |
| 78 Pt | 190 | 0.014 | 6.5 × 1011 | α | 3.24 |
| 83 Bi | 209 | 100 | 1.9 x 1019 | α | 3.1373 |
| 90 Th | 232 | 100 | 1.4 × 1010 | α | 4.08 |
| 92 U | 235 | 0.720 | 7.0 × 108 | α | 4.68 |
| 92 U | 238 | 99.27 | 4.5 × 109 | α | 4.27 |
a EC = electron capture. The EC energy is between ground states, but, in 138La decay, 1.44 MeV of the EC energy goes to a gamma ray that feeds the ground state.
b Indirect evidence for β- β- decay.
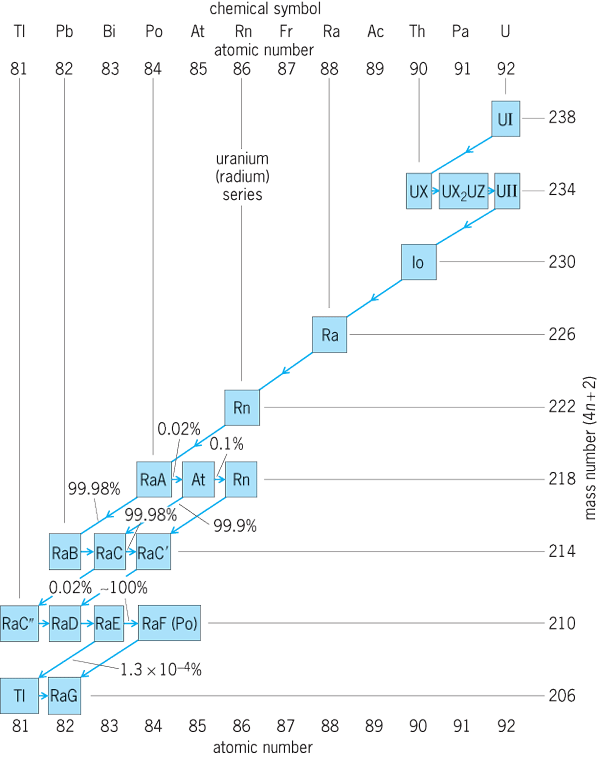
Uranium-238 decays through a long series of 14 radioactive decay products before ending as a stable isotope of lead, 206Pb. Some of these members of the 238U decay chain have very short half-periods, so their existence in nature is entirely dependent on the presence of their long-lived parent, and thus is a genealogical accident. For example, radium occurs in nature only in the minerals of its parent, uranium. The decay series of 235U supports 14, and the decay series of 232Th supports 10, short-lived radioactive substances found in nature.
A few of the common elements contain long-lived, naturally radioactive isotopes. For example, all terrestrial potassium contains 0.012% of the radioactive isotope 40K, which has a half-period of 1.3 × 109 years, and emits negatron or positron beta particles (plus decay via electron capture) and gamma rays in a dual decay to stable 40Ca and 40Ar. This isotope is the principal source of radioactivity in a normal human being; each human contains about 0.1 microcurie (3.7 × 103 becquerels) of the radioactive potassium isotope 40K.
Geological age measurements are based on the accumulation of decay products of long-lived isotopes, especially in the cases of 40K, 87Rb, 232Th, 235U, and 238U.
Laboratory-produced radioactive nuclei
With particle accelerators and nuclear reactors, of the order of 2500 radioactive isotopes not found in detectable quantities in the Earth's crust have been produced in the laboratory since 1935, including those of 26 new chemical elements up to element 118. Earlier titles of induced or artificial radioactivities for these isotopes are misnomers. Many of these now have been identified in meteorites and in stars, and others are produced in the atmosphere by cosmic rays. There are over 5000 isotopes theoretically predicted to exist. As one approaches the place where a proton or neutron is no longer bound in a nucleus of an element (the limits of the existence of that element), the half-periods become extremely short. See also: Transuranium elements
For example, carbon-14 is a negatron beta-particle emitter, with a half-period of about 5600 years, which can be produced in the laboratory as the product of a variety of different nuclear transmutation experiments. Nuclear bombardment of 11B nuclei by alpha particles (helium nuclei) can produce excited compound nuclei of 15N which promptly emit a proton (hydrogen nucleus), leaving 14C as the end product of the transmutation. The same end-product 14C can be produced by bombarding 14N with neutrons, resulting in nuclear reaction (18).
This reaction is easily carried out by using neutrons from nuclear accelerators or a nuclear reactor. This particular transmutation reaction is one which occurs in nature also, because the nitrogen in the Earth's atmosphere is continually bombarded by neutrons which are produced by cosmic rays, thus producing radioactive 14C. Mixing of 14C with stable carbon provides the basis for radiocarbon dating of systems that absorb carbon for times up to about 50,000 years ago (10 half-lives). See also: Cosmic ray; Nuclear reaction; Nuclear reactor; Particle accelerator; Radiocarbon dating
Radioactive hydrogen, 3H, is also formed in the atmosphere from the 14N + neutron →12C + 3H reaction. Also, 3H is produced in the Sun, and the Earth's water as well as satellites show an additional concentration of 3H from the Sun. Over two dozen radioactive products, ranging in half-life from a few days to millions of years, have been identified in meteorites that have fallen to Earth. The carbon and hydrogen burning cycles that produce energy for stars produce radioactive 13N, 15O, 3H. At higher temperatures the radioactivities 7Be and even 8Be (T ≈ 10−16 s) help burn hydrogen and helium. In addition to the production of radioactive as well as stable isotopes prior to the formation of the solar system, nucleosynthesis continues to go on in stars with the production of many short-lived radioactive atoms by different processes. See also: Carbon-nitrogen-oxygen cycles (astrophysics); Nucleosynthesis; Proton-proton chain
The yield of any radioactivity produced in the laboratory is the initial rate of the activity under the particular conditions of nuclear bombardment. When a target material A is bombarded to produce a radioactive product B whose radioactive decay constant is λB, the number of atoms B which are present after a bombardment of duration t, and their activity BλB, are given by Eq. (19),
where the yield Y has dimensions equivalent to curies of activity produced per second of bombardment. The yield Y depends on the number of atoms A present in the target, the intensity of the beam of bombarding particles, and the cross section, or probability of the reaction per bombarding particle under the conditions of bombardment.
Radioactive transformation series
As noted in Eqs. (12)–(14), many radioactive substances have decay products which are also radioactive. Accordingly, many long chains or series of radioactive transformations are known. The three naturally occurring transformation series are headed by 232Th, 235U, and 238U (Fig. 4 and Table 3).
| Early nameb | Early symbolb | Atomic number | Mass number | Isotopic symbol | Half-period | Type of decay |
|---|---|---|---|---|---|---|
| Uranium (4n + 2) series | ||||||
| Uranium I | UI | 92 | 238 | 238U | 4.5 × 109 y | α, SF |
| Uranium X1 | UX1 | 90 | 234 | 234Th | 24 d | β- |
| Uranium X2 | UX2 | 91 | 234 | 234mPa | 1.2 m | IT, β- |
| Uranium Z | UZ | 91 | 23 | 234Pa | 6.7 h | β- |
| Uranium II | UII | 92 | 234 | 234U | 2.5 × 105 y | α |
| Ionium | Io | 90 | 230 | 230Th | 7.5 × 104 y | α |
| Radium | Ra | 88 | 226 | 226Ra | 1600 y | α |
| Radon | Rn | 86 | 222 | 222Rn | 3.8 d | α |
| Radium A | RaA | 84 | 218 | 218Po | 3.1 m | α |
| Radium B | RaB | 82 | 214 | 214Pb | 27 m | β- |
| Radium C | RaC | 83 | 214 | 214Bi | 20 m | β-, α |
| Radium C? | RaC? | 84 | 214 | 214Po | 1.6 × 10-4 s | α |
| Radium C? | RaC? | 81 | 210 | 210Tl | 1.3 m | β- |
| Radium D | RaD | 82 | 210 | 210Pb | 22 y | β- |
| Radium E | RaE | 83 | 210 | 210Bi | 5.0 d | β-, α |
| Radium F | RaF | 84 | 210 | 210Po | 138 d | α |
| Thallium | Tl | 81 | 206 | 206Tl | 4.2 m | β- |
| Radium G | RaG | 82 | 206 | 206Pb | Stable | Stable |
| Thorium (4n) series | ||||||
| Thorium | Th | 90 | 232 | 232Th | 1.4 × 1010 y | α |
| Mesothorium1 | MsTh1 | 88 | 228 | 228Ra | 5.8 y | β- |
| Mesothorium2 | MsTh2 | 89 | 228 | 228Ac | 6.1 h | β- |
| Radiothorium | RdTh | 90 | 228 | 228Th | 1.9 y | α |
| Thorium X | ThX | 88 | 224 | 224Ra | 3.6 d | α |
| Thoron | Tn | 86 | 220 | 220Rn | 56 s | α |
| Thorium A | ThA | 84 | 216 | 216Po | 0.15 s | α |
| Thorium B | ThB | 82 | 212 | 212Pb | 10.6 h | β- |
| Thorium C | ThC | 83 | 212 | 212Bi | 1.0 h | β-, α |
| Thorium C? | ThC? | 84 | 212 | 212Po | 3 × 10-7 s | α |
| Thorium C? | ThC? | 81 | 208 | 208Tl | 3.1 m | β- |
| Thorium D | ThD | 82 | 208 | 208Pb | Stable | Stable |
| Actinium (4n + 3) series | ||||||
| Actinouranium | AcU | 92 | 235 | 235U | 7.0 × 108 y | α, SF |
| Uranium Y | UY | 90 | 231 | 231Th | 26 h | β- |
| Protactinium | Pa | 91 | 231 | 231Pa | 3.3 × 104 y | α |
| Actinium | Ac | 89 | 227 | 227Ac | 22 y | β-, α |
| Radioactinium | RdAc | 90 | 227 | 227Th | 19 d | α |
| Actinium K | AcK | 87 | 223 | 223Fr | 22 m | β-, α |
| Actinium X | AcX | 88 | 223 | 223Ra | 11 d | α |
| Astatine | At | 85 | 219 | 219At | 0.9 m | α, β- |
| Actinon | An | 86 | 219 | 219Rn | 4.0 s | α |
| Actinium A | AcA | 84 | 215 | 215Po | 1.8 × 10-3 s | α |
| Actinium B | AcB | 82 | 211 | 211Pb | 36 m | β- |
| Actinium C | AcC | 8 | 211 | 211Bi | 2.1 m | α, β- |
| Actinium C? | AcC? | 84 | 211 | 211Po | 0.5 s | α |
| Actinium C? | AcC? | 81 | 207 | 207Tl | 4.8 m | β |
| Actinium D | AcD | 82 | 207 | 207Pb | Stable | Stable |
a Radon-223 has been shown to have a very weak radioactive 14C decay branch to 209Pb. Several of the isotopes in these chains, such as 234,235,238U, 226Ra, and others are predicted to have such very weak, heavy cluster decay branches (see Table 1).
b These were the names and symbols used before the different isotopes of these elements were known.
Each of the naturally occurring radioactive isotopes in these transformation series has two synonymous names. For example, the commercially important radioisotope whose classical name is mesothorium-1 is known to be an isotope of radium with mass number of 228 and is designated as radium-228 (228Ra). Table 3 summarizes the names, symbols, and some radioactive properties of these three transformation series. However, these chains are not the only ones. Their uniqueness or importance as chains is an accident of the very long half-lives of 232Th, 235U, and 238U. For example, element 105 of mass 260 has a succession of seven alpha decays and one electron capture and positron decay to 232Th. The special importance of the chains in Table 3 is related to the fact that they were essentially the only early sources of radioactive materials, and they also play a role in nuclear power. See also: Nuclear power
Transformation series are now known for every element in the periodic table except hydrogen. Chains of neutron-rich isotopes have been produced and studied among the products of nuclear fission. Heavy-ion-induced reactions and high-flux reactors have been used to extend knowledge of the elements beyond uranium. The elements from number 93 (neptunium) to 118 (oganesson), which have so far not been found on Earth, were made in the laboratory. Both proton- and heavy-ion-induced reactions have extended knowledge of chains and neutron-deficient isotopes of the stable elements.
Alpha-particle decay
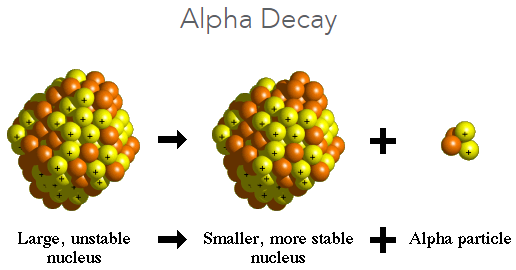
Alpha-particle decay refers to when a parent nucleus expels an alpha particle (a helium nucleus), which contains two protons and two neutrons. Thus, the atomic number, or nuclear charge Z, of the decay product is 2 units less than that of the parent, and the nuclear mass A of the product is 4 atomic mass units less than that of the parent, because the emitted alpha particle carries away this amount of nuclear charge and mass. The decrease of 2 units of atomic number or nuclear charge between parent and product means that the decay product will be a different chemical element, displaced by 2 units to the left in the periodic table of the elements. For example, radium has atomic number 88 and is found in column 2 of the periodic table. Its decay product after the emission of an alpha particle is a different chemical element, radon, whose atomic number is 86 and whose position is in the last column of the periodic table as a noble gas.
The alpha particle is emitted with a speed of the order of 1 to 2 × 107 m/s (104 mi/s), that is, about 1/20 of the velocity of light. In the simplest case of alpha decay, every alpha particle would be emitted with exactly the same velocity and hence the same kinetic energy. However, in most cases there are two or more discrete energy groups called lines (Fig. 5). For example, in the alpha decay of a large group of 238U atoms, 77% of the alpha decays will be by emission of alpha particles whose kinetic energy is 4.20 MeV, while 23% will be by emission of 4.15-MeV alpha particles. When the 4.20-MeV alpha particle is emitted, the decay product nucleus is formed in its ground (lowest energy) level. When a 4.15-MeV alpha particle is emitted, the decay product is produced in an excited level, 0.05 MeV above the ground level. This nucleus promptly transforms to its ground level by the emission of a 0.05-MeV gamma ray or alternatively by the emission of the same amount of energy in the form of a conversion electron and the associated spectrum of characteristic x-rays. Thus, in all alpha-particle spectra, the alpha particles are emitted in one or more discrete and homogeneous energy groups, and alpha-particle spectra are accompanied by gamma-ray and conversion electron spectra whenever there are two or more alpha-particle groups in the spectrum.
Geiger-Nuttall rule
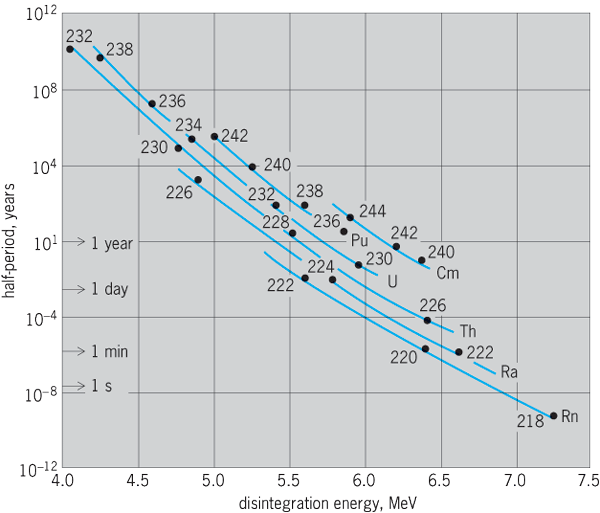
Among all the known alpha-particle emitters, most alpha-particle energy spectra lie in the domain of 4–6 MeV, although a few extend as low as 2 MeV (14762Sm) and as high as 10 MeV (21284Po or ThC′). There is a systematic relationship between the kinetic energy of the emitted alpha particles and the half-period of the alpha emitter. The highest-energy alpha particles are emitted by short-lived nuclides, and the lowest-energy alpha particles are emitted by the very long lived alpha-particle emitters. The German physicist Hans Geiger and the English physicist John Mitchell Nuttall showed that there is a linear relationship between log λ and the energy of the alpha particle.
The Geiger-Nuttall rule is inexplicable by classical physics but emerges clearly from quantum, or wave, mechanics. In 1928, the hypothesis of transmission through nuclear potential barriers, as introduced by Russian-born U.S. physicist George Gamow and independently by British theoretical physicist Ronald Wilfred Gurney and U.S. nuclear physicist Edward Condon, was shown to give a satisfactory account of the alpha-decay data, and it has been altered subsequently only in details. The form of the barrier-penetration equations is such that correlation plots of log λ against 1/E give nearly straight lines. See also: Quantum mechanics
Nuclear potential barrier
At distances r which are large compared with the nuclear radius, the potential energy of an alpha particle, whose charge is 2e, in the field of a residual nucleus whose charge is (Z − 2)e, is 2(Z − 2)e2/r. At very close distances, this electrostatic repulsion is opposed and overcome by short-range, nuclear, attractive forces. The net potential energy U as a function of the separation r between the alpha particle and its residual nucleus is the nuclear potential barrier.
One of several operating definitions of the nuclear radius R is the distance r = R at which the attractive nuclear forces just balance the repulsive electrostatic forces. At this distance, called the top of the nuclear barrier, the potential energy is about 25–30 MeV for typical cases of heavy, alpha-emitting nuclei (Fig. 6).
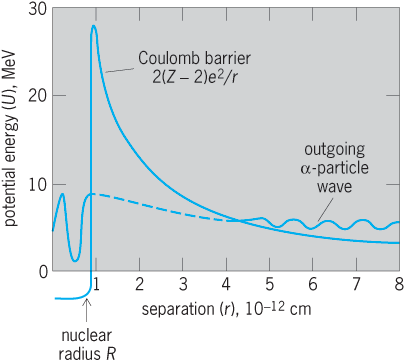
Inside the nucleus, the alpha particle is represented as a de Broglie matter wave. According to wave mechanics, this wave has a very small but finite probability of being transmitted through the nuclear potential energy barrier and thus of emerging as an alpha particle emitted from the nucleus. The transmission of a particle through such an energy barrier is completely forbidden in classical electrodynamics but is possible according to wave mechanics. This transmission of a matter wave through an energy barrier is analogous to the familiar case of the transmission of ordinary visible light through an opaque metal such as gold: if the gold is thin enough, some light does get through, as in the case of the thin gold leaf which is sometimes used for lettering signs on store windows. See also: Quantum mechanics
The wave-mechanical probability of the transmission of an alpha particle through the nuclear potential barrier is very strongly dependent upon the energy of the emitted alpha particle. Analytically, the probability of transmission T depends exponentially upon a barrier transmission exponent γ according to Eq. (20).
To a good approximation, Eq. (21) holds,
where h = 6.626 × 10−34 joule-second is Planck's constant, and M is the so-called reduced mass of the alpha particle. For the alpha decay of 226Ra, the numerical value of γ is about 71: hence T = e−71 = 10−31. The first term on the right side of Eq. (21) is about 154 and is therefore the dominant term. When this term is taken alone, e−(4π2/h)(Z−2)2e2/V is called the Gamow factor for barrier penetration. See also: Planck's constant
Inspection of Eq. (21) shows that the barrier transmission decreases with increasing nuclear charge (Z − 2)e, increases with increasing velocity V of emission of the alpha particle, and increases with increasing radius R of the nucleus. When the experimentally known values of alpha-decay energy are substituted into Eq. (21), with R about 10−12 cm and Z about 90, the transmission coefficient T = e−λ is found to extend over a domain of about 10−20 to 10−40. This range of about 1020 is just what is needed to relate the alpha-decay energy to the broad domain of known alpha-decay half-periods. Equation (21) thus explains the Geiger-Nuttall rule very successfully (Fig. 7). From Eq. (20), one can derive the relationship between the mean life τ in seconds and the alpha-particle energy Eα in MeV, ln τ = AE−1/2α + B, where A and B are constants for different parent nuclei. From Fig. 7 it may be noted that, if the alpha decay energies of 232Th and 235,238U had been 0.2 to 0.5 MeV higher, their half-lives would have been too short for them to still be present in the Earth's crust. If that had been the case, then radioactivity and the nucleus of the atom might never have been discovered.
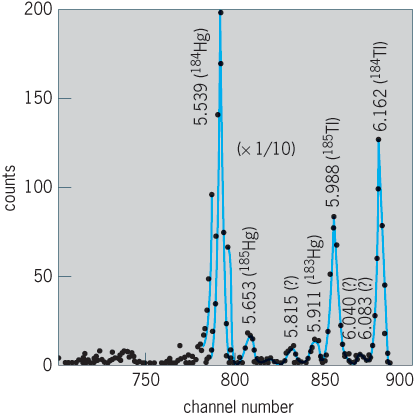
Knowledge of alpha-emitting isotopes was greatly enlarged through the identification of many isotopes' far off stability in the region just above tin and in the broad region from neodymium all the way to uranium. For example, fusion reactions between 290-MeV 58Ni ions and 58Ni and 63Cu targets have been used to produce and study very neutron deficient radioactive isotopes, including 12 alpha emitters between tin and cesium. These results provide important data on the atomic masses of nuclei far from the stable ones in nature. These data test understanding of nuclear mass formulas and their validity in new regions of the periodic table.
Beta-particle decay
Beta-particle decay is a type of radioactivity in which the parent nucleus emits a beta particle. There are two types of beta decay established: in negatron beta decay (β−) the emitted beta particle is a negatively charged electron (negatron); in positron beta decay (β+) the emitted beta particle is a positively charged electron (positron). In beta decay, the atomic number shifts by one unit of charge, while the mass number remains unchanged (Table 1). In contrast to alpha decay, when beta decay takes place between two nuclei which have a definite energy difference, the beta particles from a large number of atoms will have a continuous distribution of energy (Fig. 8). See also: Positron
For each beta-particle emitter, there is a definite maximum or upper limit to the energy spectrum of beta particles. This maximum energy, Emax, corresponds to the change in nuclear energy in the beta decay. Thus Emax = 0.57 MeV for β− decay of 64Cu, and Emax = 0.66 MeV for β+ decay of 64Cu. For positron decay to occur, the total decay energy must exceed 1.022 MeV (twice the rest energy of the electron). The total decay energy for β+ decay is then Emax (β+) plus 1.022 MeV. As in the case of alpha decay, most beta-particle spectra are not this simple, but include additional continuous spectra which have less maximum energy and which leave the product nucleus in an excited level from which gamma rays are then emitted.
For nuclei very far from stability, the energies of these excited states populated in beta decay are so large that the excited states may decay by proton, two-proton, neutron, two-neutron, three-neutron or alpha emission, or spontaneous fission. In some cases, the energies are so great that the number of excited states to which beta decay can occur is so large that only the gross strength of the beta decays to many states can be studied.
Neutrinos
The continuous spectrum of beta-particle energies (Fig. 8) implies the simultaneous emission of a second particle besides the beta particle, in order to conserve energy and angular momentum for each decaying nucleus. This particle is the neutrino. The sum of the kinetic energy of the neutrino and the beta particle equals Emax for the particular transition involved except in the rare cases where internal bremsstrahlung or shake-off electrons are emitted along with the beta particle and neutrino. The neutrino has zero charge and nearly zero rest mass, travels at essentially the same speed as light (3 × 108 m/s or 1.86 × 105 mi/s), and is emitted as a companion particle with each beta particle. See also: Neutrino
Two forms of neutrinos are distinguished in beta decay. In positron beta decay, a proton p in the nucleus transforms into a neutron n in the nucleus, thus reducing the nuclear charge by 1 unit. At the time of this transition, two particles, the positron β+ and the neutrino ν, are created and emitted. The emitted β+ and ν together carry away the energy Emax of the transition and provide for conservation of energy, momentum, angular momentum, charge, and statistics. Thus positron beta decay is represented by decay (22).
Negatron beta decay is a closely related process, except that a neutron n changes to a proton p in the nucleus, and a negatron beta particle β− and its characteristic companion particle, the antineutrino, are emitted, as in decay (23).
The antineutrino is the antiparticle of the neutrino as the β+ is the antiparticle of the β−. The ν and have the same properties of zero charge and essentially zero rest mass, and differ only with respect to the direction of alignment of their intrinsic spin along their direction of motion. In most beta-decay contexts, the term “neutrino” includes both its forms, neutrino and antineutrino. See also: Antimatter
There are, in fact, three classes of neutrinos. The neutrinos emitted in the two types of beta decay (the decays in equations 22 and 23) are called electron neutrinos. In addition, there is a neutrino and antineutrino associated with the mu meson (μ±) and neutrinos and antineutrinos associated with the tau (τ±). These three particles, electron, mu, and tau, together with their neutrinos, νe, νμ, and ντ, and their respective antiparticles, make up a class of particles called leptons. The number of leptons in a decay or reaction is considered to be conserved; this rule is called lepton number conservation. There are separate conservation numbers for e, μ, and τ. There must be the same net number of each type of lepton on each side of a decay or reaction. For example, because there are no leptons on the left sides of the decays in equations 22 and 23, there must be no net leptons on the right sides. Thus the decay in equation 22 has on the right side an antielectron (positron) with lepton number L = −1 and a neutrino with lepton number L = 1. The decay in equation 23 has an electron with L = 1 and an antineutrino with L = −1, and so the lepton number is L = 1 − 1 = 0 leptons on the right side as well. The decays in equations 22 and 23 also conserve nucleon number. A nonzero rest mass of neutrinos opens up the possibility of neutrons oscillating from νe to νμ or vice versa, as well as from νμ to and other types, as required in grand unified theories. See also: Lepton
Because the neutron rest mass is greater than the proton rest mass, free neutrons can undergo beta decay (in decay in equation 23), but protons must use part of the nuclear binding energy available inside a nucleus to make up the rest mass difference in the decay in equation 22.
The interaction of neutrinos with matter is exceedingly feeble. A neutrino can pass all the way through the Sun with little chance of collision. The thickness of lead required to attenuate neutrinos by the factor 1/2 is about 1018 m (1015 mi), or 100 light-years of lead. See also: Light-year
Average beta energy
Charged particles, such as beta particles or alpha particles, are easily absorbed in matter, and their kinetic energy is thereby converted into heat. In beta decay, the average energy Eav of the beta particles is far less than the maximum energy Emax of the particular beta-particle spectrum. The detailed shape of beta-particle spectra and hence the exact value of the ratio Eav /Emax varies somewhat with Z, Emax, the degree of forbiddenness of the transition, and the sign of charge of the emitted beta particle. A rough rule of thumb which covers many practical cases is Eav = (0.40 ± 0.05)Emax, with slightly higher values for positron beta-particle spectra than for negatron beta-particle spectra. The remaining decay energy is emitted as kinetic energy of neutrinos and is not recoverable in finite absorbers.
There are other processes that carry off part of the energy of beta decay, including internal bremsstrahlung (gamma rays) and shake-off electrons (atomic electrons). The total probabilities for these additional two processes are on the order of 1% or much less per beta decay, and the probability of their emission decreases rapidly with increasing energy, so they are mainly low-energy (less than about 50 keV) radiations. In internal bremsstrahlung, through an interaction of the beta particle and the emitting nucleus, part of the decay energy is emitted as a gamma ray. In the shake-off process, part of the beta-decay energy is given to one of the atomic electrons. The gamma rays are not absorbed in matter as easily as the beta particles. In addition, if one tries to absorb the beta particles in matter, the beta particles can interact with the atoms and give off external bremsstrahlung (gamma rays). The number of these gamma rays again is a strongly decreasing function of energy, but their emission extends up to the maximum energies of the beta particles. See also: Bremsstrahlung
Fermi theory
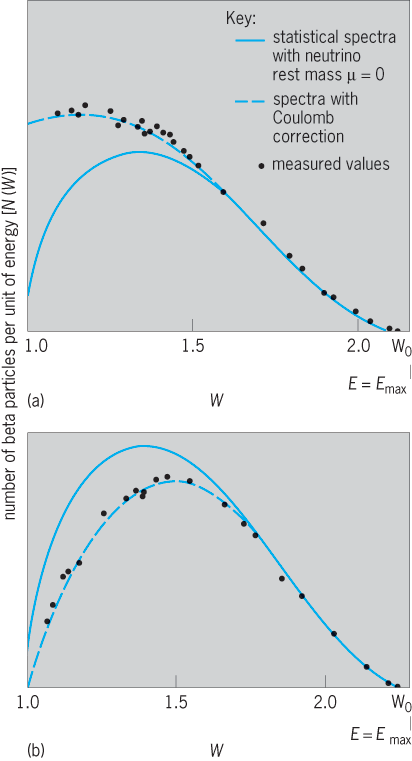
By postulating the simultaneous emission of a beta particle and a neutrino, as in reaction (22), Italian-born U.S. physicist Enrico Fermi developed in 1934 a quantum-mechanical theory which satisfactorily gives the shape of beta-particle spectra (Fig. 8), and the relative half-periods of beta-particle emitters for allowed beta decays. The energy distribution of beta particles in allowed transitions is then given by Eq. (24).
Here N(W) dW = number of beta particles in energy range W to W + dW; W = 1 + E/(m0 c2) = total energy of beta particle in units of rest energy m0 c2 = 0.51 MeV for an electron (m0 = electron mass, c = velocity of light); W0 = 1 + Emax/(m0 c2) = maximum energy of the beta-particle spectrum; |P|2 = squared matrix element for the transition, and is of the order of unity for allowed transitions; τ0 = time constant ≈ 7000 s; F(Z,W) = complex, dimensionless function involving the nuclear radius, nuclear charge, beta-particle energy, and whether the decay is β− or β+.
Physically, this distribution function involves the product of the energy W and momentum (W2− 1)1/2 of the beta particle times the energy (W0 − W) and the momentum (W0 − W)/c of the neutrino. The product of these factors gives a “statistical” distribution for the number of beta particles as a function of energy (Fig. 8). The observed spectra show an excess of low-energy β− and a deficiency of low-energy β+ particles. This arises because of the Coulomb attraction and repulsion of the nucleus for β− and β+. The statistical spectrum is corrected by the Fermi function, F(Z,W), and the new distribution agrees with experiments (Fig. 8).
Equation (24) essentially matches the energy spectra of allowed beta-particle transitions and therefore furnishes one type of experimental verification of the properties of neutrinos. Its counterpart in terms of the beta-particle momentum spectrum is often used for the analysis of spectra, and is given by Eq. (25).
The momentum distribution is much more nearly symmetric than its corresponding energy spectrum. Here N(η)dη = number of beta particles in the momentum interval from η to η + dη; η = (W2− 1)1/2 = momentum of the beta particle in units of m0 c; and F(Z,η) = F(Z,W) of Eq. (24).
Konopinski-Uhlenbeck theory
After the work of Fermi which explained allowed decay, Polish-born U.S. nuclear physicist Emil John Konopinski and Dutch-born U.S. theoretical physicist George Uhlenbeck in 1941 developed the theory of forbidden beta decay. Allowed decays occur between nuclear states which differ in spin by 0 or 1 unit and which have the same parity. Konopinski and Uhlenbeck developed a theory to describe beta decays where energy is available for decay but the allowed selection rules on spin or parity or both are violated. These beta transitions occur at a slower rate and are called forbidden transitions. In 1949, the theory of forbidden beta decay was confirmed by U.S. nuclear physicist Lawrence Langer and U.S physicist H. Clay Price Jr. The orders of forbiddenness, which retard the rate of decay, are the following: once-forbidden decay when the change in nuclear spin ΔJ is again 0 or 1 as in allowed decay, but a parity change Δπ occurs; once-forbidden unique decay when Δπ changes and ΔJ = 2; n-times forbidden decay when ΔJ = n, Δπ = (−)n, where Δπ = − indicates a parity change; and n-times forbidden unique decay when ΔJ = n + 1, Δπ = (−)n [Table 4]. In forbidden decays, the first-order allowed matrix elements of the Fermi theory in Eq. (24) vanish because of the selection rules on angular momentum and spin. Then the much smaller higher-order matrix elements that can be neglected compared to the large allowed matrix elements come into play. See also: Parity (quantum mechanics); Selection rules (physics)
| Type | ΔJ | Δπ | Log fT | Examples |
|---|---|---|---|---|
| Allowed (favored) | 0 or 1 | No | 3 | n, 3H |
| Allowed (normal) | 0 or 1 | No | 4 to 6 | 35S, 30P |
| Allowed (favored) | 0 or 1 | No | 3 | 35S, 30P |
| Allowed (I-forbidden) | 1 | No | 5 to 8 | 32P, 65Ni |
| Once-forbidden | 0 or 1 | Yes | 5 to 9 | 111Ag, 143Pr |
| Once-forbidden (unique) | 2 | Yes | 7 to 10 | 42K, 91Y |
| Twice-forbidden | 2 | No | 11 to 14 | 36Cl, 59Fe |
| Twice-forbidden (unique) | 3 | No | 12 to 14 | 22Na, 60Co |
| Third-forbidden | 3 | Yes | 17 to 19 | 87Rb, 138La |
| Third-forbidden (unique) | 4 | Yes | (∼18) | 40K |
| Fourth-forbidden | 4 | No | ∼24 | 115In |
| Fourth-forbidden (unique) | 5 | No |
Comparative half-lives, fT
The half-period T of beta decay can be derived from Eq. (24) because the radioactive decay constant λ = 0.693/T is simply the total probability of decay, or N(W) dW integrated over all possible values of the beta-particle energy from W = 1 to W = W0.
For allowed decays, the matrix elements are not functions of the beta energy and can be factored out of Eq. (24), so Eq. (26) is valid,
where f is given by Eq. (27),
and the constants include |P|2 of Eq. (24). Equation (26) can be rearranged as Eq. (28).
For different beta decays, T varies over a range greater than 1018 and inversely depends on the beta-decay energy in analogy to the Geiger-Nuttall rule for alpha decay. However, Eq. (28) says that the comparative half-life should be a constant. Indeed, it is found experimentally that different classes of beta decay do have very similar fT values. It is generally easier to give the log10 fT for comparison. The groups (Table 4) include, in addition to the forbidden decays, three classes of allowed decays: the favored or superallowed decays of nuclei whose structures are very similar so that the matrix element in the denominator of Eq. (28) is large and log fT is small; normal allowed; and allowed I-forbidden where the total angular momentum selection rule holds, but the individual particle that is undergoing beta decay has a change of 2 units of orbital angular momentum. The matrix elements for each degree of forbiddenness get progressively smaller and so log fT values increase sharply with each degree of forbiddenness. The ranges of these fT values for each degree of forbiddenness are in general so well established that measurements of fT values can be used to establish changes in spins and parities between nuclear states in beta decay.
Kurie plots
For allowed transitions, the transition matrix element |P|2 is independent of the momentum η. Then Eq. (25) can be put in the form of Eq. (29).
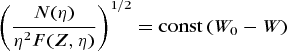 (29)
(29)Therefore, a straight line results when the quantity (N/η2 F)1/2 is plotted against beta-particle energy, either as W or as E, on a linear scale. Such graphs are called Kurie plots, Fermi plots, or Fermi-Kurie plots. These are especially useful for revealing deviations from the allowed theory and for obtaining the upper energy limit Emax as the extrapolated intercept of N/η2 F on the energy axis. Practically all of the results on the shapes of beta-particle spectra are published as Kurie plots, rather than as actual momentum or energy spectra.
When spectral data give a straight line, then N(η) is in agreement with the Fermi momentum distribution, Eq. (25); and the intercept of this straight line, on the energy axis, gives the decay energy Emax. For β+ decay the total decay energy is Emax (β+) plus 1.022 MeV. In a, theoretical curves are given for various values of the neutrino rest mass, and the data points, which are experimental values, lie on the curve corresponding to zero mass.
In addition to allowed decays, all but one known once-forbidden decays have Kurie plots that are essentially linear in energy (b). The once-forbidden unique decays have a pronounced characteristic energy dependence for their matrix elements, and thus the conventional Kurie plot has a characteristic shape that differs from a straight line (Fig. 9). When the data are corrected by the unique shape factor, given by Konopinski and Uhlenbeck, a linear Kurie plot is again obtained. This unique shape was the key to the discovery of forbidden beta decay by Langer and Price (Fig. 9). The higher-order forbidden spectra each show different strong energy dependencies in their Kurie plots, each characteristic of their degree of forbiddenness.
Double-beta decay
When the ground state of a nucleus differing by two units of charge from nucleus A has lower energy than A, then it is theoretically possible for A to emit two beta particles, either β+β+ or β−β− as the case may be, and two neutrinos or antineutrinos, and go from Z to Z ± 2. Here, two protons decay into two neutrons, or vice versa. This is a second-order process and so should go much slower than beta decay. There are a number of cases where such decays should occur, but their half-lives are of the order of 1020 years or greater. Such decay processes are obviously very difficult to detect.
The first direct evidence for two-neutrino double-beta-minus decay of selenium, reaction (30),
was found in 1987, some 40 years after the first attempt to observe this rare process. The trajectories of the electrons from this decay were detected in a time-projection chamber with a half-period of 0.92 ± 0.07 × 1020 y obtained. Previous geochemical and cosmochemical evidence of double-beta decay had been only indirect because it consisted of observations of buildup of the noble gases 8232Kr and 13054Xe in the 8432Se and 13052Te samples, respectively. Now there are 14 known isotopes that are observed to undergo double-beta decay with half-lives that range from 8.5 × 1018 to 2.2 × 1024 y. See also: Time-projection chamber
Some unifications of the electroweak and strong forces suggest that the electron neutrino and antineutrino are identical (νe ≡ e), that is, that the neutrino is a Majorana particle. There is no experimental evidence at present for this. If true, this allows double-beta decay to proceed without the emission of neutrinos. In this neutrinoless double-beta decay, the first neutrino absorbs the second one so the decay is decay (31).
Extensive searches to discover such decays have shown that the half-period of this decay is greater than 0.9 × 1026 y. Lepton number is not conserved in the decay in equation 31. This process is predicted to occur in some grand unified theories. See also: Double-beta decay; Grand unification theories
Electron-capture transitions
Whenever it is energetically allowed by the mass difference between neighboring isobars, a nucleus Z may capture one of its own atomic electrons and transform to the isobar of atomic number Z − 1 (Table 1). Usually the electron-capture (EC) transition involves an electron from the K shell of atomic electrons, because these innermost electrons have the greatest probability density of being in or near the nucleus. See also: Electron capture
In EC transitions, a proton p bound in the parent nucleus absorbs an electron e− and changes to a bound neutron n. The decay energy is carried away by an emitted neutrino ν as in transition (32).
The residual nucleus may be left either in its ground level or in an excited level from which gamma-ray emission follows. EC transitions compete with all cases of positron beta-particle decay. EC has an energetic advantage over β+ decay equivalent to the mass of two electrons, or 1.02 MeV, because in transition in equation 32, one electron mass e− enters on the left and is available, whereas in the decay in equation 22, one electron mass β+ must be produced as a product of the positron beta-particle decay. For example, in the radioactive decay of 6429Cu, twice as many transitions go by EC to 6428Ni as go by positron beta decay to the same decay product. In the heavy, high-Z elements, EC is greatly favored over the competing β+ decay, and examples of measurable β+ decay are practically unknown for Z greater than 80, although there are a large number of examples of electron capture. As the energy for decay increases beyond 1.02 MeV, the probability of β+ decay increases relative to EC and dominates at several megaelectronvolts of energy.
Several examples are known of completely pure EC radioactivity in which there is insufficient nuclear energy to allow any positron beta-particle decay (total decay energy is less than 1.022 MeV). For example, 5526Fe emits no positron beta particles, but transforms with a half-period of 2.6 years entirely by EC to the ground level of 5525Mn. This radioactivity is detectable through the K-series x-rays which are emitted from 55Mn when the atomic electron vacancy, produced by nuclear capture of a K electron, refills from the L shell of atomic electrons. Also, double-electron capture, analogous to double-beta decay, can occur, albeit rarely. Here two atomic electrons are captured and two neutrinos emitted.
Gamma-ray decay
Gamma-ray decay involves a transition between two excited levels of a nucleus, or between an excited level and the ground level. A nucleus in its ground level cannot emit any gamma radiation. Therefore, gamma-ray decay occurs only as a sequel of one of the processes in Table 1 or of some other process whereby the product nucleus is left in an excited state. Such additional processes include gamma rays observed following the fusion of two nuclei, as occurs in bombarding 58Ni with 16O to form an excited compound nucleus of 74Kr. This compound nucleus first promptly gives off a few particles like two neutrons to leave 72Kr* or two protons to leave 72Se*, both of which will be in excited states which will emit gamma rays. Alternatively, one may excite states in a nucleus by the Coulomb force between two nuclei when they pass close to each other but do not touch (their separation is greater than the sum of the radii of the two nuclei). There are also other nuclear reactions such as induced nuclear fission that leave nuclei in excited states to undergo gamma decay. See also: Coulomb excitation
A gamma ray is high-frequency electromagnetic radiation (a photon). The energy of a gamma ray is given by hν, where h is Planck's constant and ν is the frequency of oscillation of the wave in hertz. The gamma-ray or photon energy hν lies between 0.05 and 3 MeV for the majority of known nuclear transitions. Higher-energy gamma rays are seen in neutron capture and some reactions. See also: Electromagnetic radiation
Gamma rays carry away energy, linear momentum, and angular momentum, and account for changes of angular momentum, parity, and energy between excited levels in a given nucleus. This leads to a set of gamma-ray selection rules for nuclear decay and a classification of gamma-ray transitions as “electric” or as “magnetic” multipole radiation of multipole order 2l, where l = 1 is called dipole radiation, l = 2 is quadrupole radiation, and l = 3 is octupole, l being the vector change in nuclear angular momentum. The most common type of gamma-ray transition in nuclei is the electric quadrupole (E2). There are cases where several hundred gamma rays with different energies are emitted in the decays of atoms of only one isotope. See also: Multipole radiation
Mean life for transitions
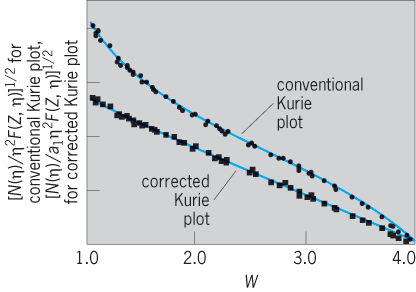
A reasonably successful approximate theory of the mean life for gamma-ray decay was developed by Austrian-born U.S. theoretical physicist Victor Weisskopf in 1951, using the single-particle shell model of nuclei (Fig. 10). An E2 transition of about 1 MeV is expected to take place with a mean life, τel, or mean delay in the upper level, of about 10−11 s. Thus, most gamma-ray transitions are prompt transitions, in which the mean life of the excited level is too short to be measured easily. The mean life τmag for magnetic multipoles is of the order of 30 (for A = 20) to 150 (for A = 200) times longer than τel for electric multipole transitions (Fig. 10).
At low energies or high Z, or both, the internal conversion process becomes a very important additional mode of decay that markedly shortens the mean lives of the nuclear levels. In addition, in many cases the structure of the nucleus comes into play and alters the observed mean lives considerably compared to those predicted by the Weisskopf theory (Fig. 10). Electric dipole (E1) transitions are generally retarded (longer mean lives) by factors of 106 over the Weisskopf estimates (Fig. 10). On the other hand, Danish physicist Aage Bohr and U.S.-born Danish nuclear physicist Benjamin Roy Mottelson developed a model of collective nuclear motions where E2 transitions are enhanced by factors of 100 or more (shorter τ) over the Weisskopf single-particle estimates, and these predictions are confirmed by experiments. The magnetic dipole (M1) transitions are also often hindered by factors of 100 or more. Measurements of the mean lives for gamma-ray decay provide important tests of nuclear models.
Internal conversion
An alternative type of deexcitation which always competes with gamma-ray emission is known as internal conversion. Instead of the emission of a gamma ray, the nuclear excitation energy can be transferred directly to a bound electron of the same atom. Then the nuclear energy difference is converted to energy of an atomic electron, which is ejected from the atom with a kinetic energy Ei given by Eq. (33).
Here Bi is the original atomic binding energy of the particular electron, which is ejected, and W is the nuclear transition energy which would otherwise have been emitted as a gamma-ray photon having energy hν = W.
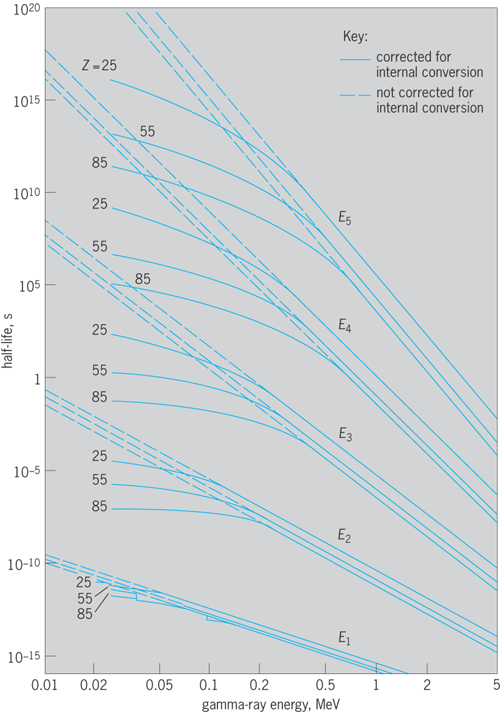
The spectrum of internal conversion electrons is then a series of discrete energies, or “lines,” each corresponding to an individual value of Bi , for the K, L (L1, L2, L3), M, … electrons in each shell and subshell of the atom. Thus conversion electron spectra are much more complex than gamma spectra (Fig. 11). From the spacing of the Ei values in this conversion electron spectrum, it is possible to assign definitely the atomic number Z of the atom in which the nuclear transition W took place. In this way it is known that the conversion electron and the competing gamma-ray emission are sequels and not antecedents of alpha decay, beta decay, and electron-capture transitions.
The total internal conversion coefficient αT is the ratio of the number of transitions proceeding by internal conversion, NeT , to the number going by gamma-ray emission, Nγ, for any particular nuclear transformation from an excited level to a lower-lying level, as in Eq. (34).
The total internal conversion coefficient is a sum of the conversion coefficients for each shell [K, L(L1 + L2 + L3), M(M1 + · · ·), and so forth], and is given by Eq. (35),
where αK = NeK Nγ, αL = NeL /Nγ = αL1 + αL2 + αL3 (αL1 = NeL1/Nγ, … ), and NeK, NeL (NeL1, … ), and so forth are the numbers of electrons ejected from the K, L (L1, L2, L3), … shells, respectively. In general, this probability of internal conversion relative to gamma-ray emission increases with increasing atomic number Z, with increasing multipole order 2l, and with decreasing nuclear deexcitation energy W. In middle-weight elements, for W = 1 MeV, α is of the order of 10−2 to 10−4; while for W = 0.2 MeV, α is of the order of 0.1 for electric l = 2 transitions, and 10 or larger for electric l = 5 transitions. When internal conversion electron decay occurs, this process is always followed by the emission of characteristic x-rays of the element and Auger electrons from outer shells when the inner shell vacancy is filled. This emission can include K x-rays, L x-rays and x-rays from higher shells, and K Auger electrons, L Auger electrons, and so forth. See also: Auger effect
Radiationless transitions
There are cases where gamma-ray emission is strictly forbidden and conversion electron emission allowed (Fig. 11). This occurs when both nuclear states have zero spin and the same parity. The conversion electrons are called electric monopole radiations, EO. These transitions occur because of the penetration of the atomic electrons into the nuclear volume where they interact directly with the nucleus. EO radiation can occur in principle whenever two states have the same spin and same parity, but in practice, EO decays are found to be very, very small in these cases. There are some exceptions in well-deformed nuclei and in nuclei which have states with quite different shapes. In these cases, EO decays can totally dominate the electron emission for transitions that have no change in spin and that involve decays between states with large differences in their nuclear shapes (Fig. 11).
The EO decays which arise because of the penetration of the atomic electrons into the nuclear volume are thus sensitive measures of changes in shape between two nuclear states, and have played important roles in establishing vibrations of the nuclear shape and the coexistence of states with quite different deformation in the same nucleus. There also are other circumstances where the penetration of the atomic electron into the nuclear volume gives rise to additional contributions to the conversion-electron decay. Again, these penetration effects probe details of the structure of the nucleus.
Internal pair formation
When the energy between two states in the same nucleus exceeds 1.022 MeV, twice the rest mass energy of an electron, it is possible for the nucleus to give up its excess energy to an electron-positron pair—a pair creation process. This is a third alternative mode to gamma decay and conversion electron decay. This process becomes more important as the gamma-ray energy increases. It is relatively unimportant below 2–3 MeV of decay energy. See also: Electron-positron pair production and annihilation
Isomeric transitions
Measurably delayed radioactive transitions from an excited level of a nucleus are known as isomeric transitions. The measurably long-lived excited level is called an isomeric or metastable level or an isomer of the ground level. What constitutes an isomer is not well-defined. The terminology arose when it was difficult to measure mean lives shorter than 10−7 s. States with longer mean lives were isomers. Now mean lives down to 10−13 s can be measured for many transitions in different nuclei, but these are not generally called isomers. The break point is simply not defined.
Figure 12 (below) shows that if the excitation energy is small (say, 0.5 MeV or less) and the angular momentum difference l is large (say, l = 3 or more), then the mean life of an excited level for gamma-ray or conversion-electron emission can be of the order of 1 s up to several years.
Most of the long-lived isomers occur in nuclei which have odd mass number A. Then either the number of protons Z in the nucleus is odd, or the number of neutrons N in the nucleus is odd. The frequency distribution of odd-A isomeric pairs, excited level and ground level, displays so-called islands of isomerism in which the odd-proton or odd-neutron number is less than 50 or less than 82. The distribution is one of several lines of evidence for closed shells of identical nucleons at N or Z = 50 or 82 in nuclei, and it plays an important role in the so-called shell model of nuclei. See also: Nuclear isomerism; Nuclear shell model and magic numbers
Spontaneous fission
Spontaneous fission involves the spontaneous breakup of a nucleus into two heavy fragments (two intermediate atomic number elements, for example, with Z = 42 and 50) and neutrons (Table 1). Spontaneous fission can occur when the sum of the masses of the two heavy fragments and the neutrons is less than the mass of the parent undergoing decay. After the discovery of fission in 1939, it was discovered that isotopes like 235,238U had very weak decay branches for spontaneous fission, with half-lives for spontaneous fission of 3 × 1017 and 8.2 × 1015 y, respectively. Some isotopes with relatively long half-lives such as 252Cf (2.6 y) have large (3.1%) spontaneous fission branching. In these cases, the nucleus can go to a lower energy state by spontaneously splitting apart into two heavy fragments of rather similar mass plus a few neutrons. This process liberates a large amount of energy compared to any other decay mode. Thus, 252Cf has become important in many applications in medicine and industry as a compact energy source, a source of neutrons or as a source of nuclear radiation, because the fragments themselves are left in excited states and so emit gamma rays. See also: Nuclear fission
An important isomeric decay mode was discovered in the early 1960s in the very heavy elements, spontaneous fission isomers. Here the nucleus in an excited state, rather than emit a gamma ray or conversion electron, spontaneously breaks apart into two heavy fragments plus neutrons exactly as in spontaneous fission. To identify these isomers, the symbol f is often placed after their atomic mass, for example, 244f95Am. Their half-lives are generally short, 10−3 to 10−9 s. It is now understood that these fission isomers are states with much larger deformation than the ground states of these isotopes. The Coulomb barrier against fission is in fact a double-hump barrier with the fission isomers in the valley at large deformation (Fig. 12). The study of these fission isomers has provided important tests of understanding of the behavior and structure of nuclei with very large deformation.
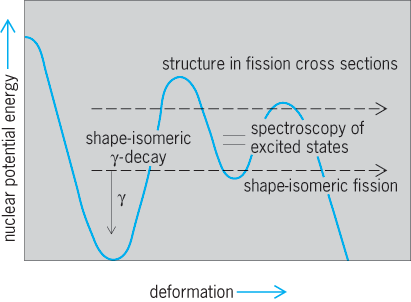
Fission with the emission of neutrons is called hot fission because the fragments have high excitation energy that is carried away by the neutron emission. In 1994, cold spontaneous fission was observed for 252Cf and, subsequently, 242Pu, in which no neutrons are emitted, in contrast to hot spontaneous fission, where one to ten neutrons are emitted. Cold ternary spontaneous fission and hot ternary spontaneous fission have also been observed. In ternary spontaneous fission, in addition to the two intermediate-mass nuclei, one light nucleus such as an alpha particle, 3H, or 6Li up to 14C, has been observed. In cold ternary spontaneous fission no neutrons are emitted, while in hot ternary spontaneous fission one or more neutrons are emitted. These rare decay modes provide new insight into the fission process, clustering in nuclei, and the theory of multifragmentation, as discussed below. See also: Nuclear fission
Heavy cluster decays
Alpha-particle decay and spontaneous fission are two natural phenomena in which an atomic nucleus spontaneously breaks into two fragments, but the fragments are of very different size in one case and almost equal size in the other. On the basis of fragmentation theory and the two-center shell model, novel kinds of radioactivities that are intermediate between alpha-particle decay and fission were predicted in 1980 by Romanian physicists Aureliu Sandulescu and Dorin Poenaru and German theoretical physicist Walter Greiner. Subsequently, it was shown theoretically that the new processes should occur throughout a very broad region of the nuclear chart, including elements with atomic numbers higher than 40. However, experimentally observable emission rates could be expected only for nuclei heavier than lead, in a breakup leading to a very stable heavy fragment with proton and neutron numbers equal or very close to Z = 82, N = 126 (20882Pb or its neighborhood).
For more than 150 kinds of cluster emission, the predicted half-periods of the parent nuclei are shorter than 1023 years. The main competitor is always alpha-particle decay. The predicted branching ratios relative to this alpha-particle decay are smaller than 10−9, with a maximum value for 146C radioactivity of 22388Ra, the first experimentally observed case. Clusters are emitted through fission processes in which the fragments retain compact shape configurations, with a relatively high kinetic energy of about 2 MeV per nucleon.
In 1984, a series of experimental confirmations began with the discovery of 146C radioactivity of 22388Ra. Initially a semiconductor telescope identification technique was used. In subsequent experiments on 146C emission from other radium isotopes, magnetic spectrometers (a superconducting solenoid and an Enge split pole) allowed suppression of the strong background of alpha particles.
Another technique uses solid-state track-recording detectors with special plastic films and glasses that are sensitive to heavier clusters but not to alpha particles. This technique has been applied to the entire range of cluster emissions measured previously and has yielded results in good agreement with theoretically predicted half-lives in the emission of 146C from radium isotopes with mass numbers 222–224 and 226; 208O from 28890Th; 239F from 23191Pa; 2410Ne from 23090Th, 23191Pa, and 232–234232–92U; 2812Mg from 23492U; and many others. See also: Particle track etching
Cluster radioactive decay to excited states of the daughter nucleus or involving excited clusters has been predicted, and experimentally verified.
In cold fission, the fragments are not very deformed or excited, just as in cluster radioactivity. Cold fission has been interpreted, according to the two-center shell model, as cluster emission. As noted above, cold fission has been clearly established in the spontaneous fission of 252Cf and 242Pu, and cold ternary spontaneous fission has also been observed. These decay modes provide tests of a unified theory that includes cold fission, light cluster radioactivity, and alpha decay.
While quite rare, these modes also provide interesting tests of the understanding of the structure of heavy nuclei, including shell and pairing effects, deformation, large-amplitude collective motion, and clustering, with particular emphasis on very heavy clusters like 13250Sn and 20882Pb. Because of its particularly strong shell effects, the 20882Pb cluster is involved not only in cluster decays but also in the asymmetric cold fusion process, which has been used in the synthesis of the heaviest elements. See also: Copernicium
Proton radioactivity
Proton radioactivity is a mode of radioactive decay that is generally expected to arise in proton-rich nuclei far from the stable isotopes, in which the parent nucleus changes its chemical identity by emission of a proton in a single-step process. Its physical interpretation parallels almost exactly the quantum-mechanical treatment of alpha-particle decay. Although proton radioactivity had been of considerable theoretical interest since 1951 and was expected to be a general phenomenon, for many years only a few examples of this decay mode were observed, because of the narrow range of half-lives and decay energies where this mode can compete with other modes. However, in the late 1990s, experimental techniques using new recoil mass spectrometers, which can separate rare reaction products, and new double-sided silicon strip detectors became available and opened up the discovery of many new proton radioactivities.
The first nuclide found, in 1970, to decay by proton radioactivity was 53m27Co (Fig. 13), where the m (metastate) denotes a (relatively) long-lived isomeric state. Because of its very high angular momentum of 19/2 and odd parity, gamma decay is highly forbidden. This mode of decay is essentially the same as that of β-delayed proton emission discussed below, except that the energy of the excited nuclear level is low, and angular momentum selection rules highly forbid gamma-ray decay so the state lives a relatively long time in comparison to those states populated in beta decay. It was produced in the laboratory by the compound nucleus reactions 168O + 4020Ca → 53m27Co + p + 2n and 5424F + p → 53m27Co + 2n. This 247-ms isomer exhibits two different decay modes: though it predominantly decays by positron (β+) emission to a similar 19/2− level in 5326Fe, a 1.5% branch in its decay occurs via direct emission of a 1.59-MeV proton to the 5226Fe ground state. The calculated half-life that 53m27Co would possess if proton radioactivity were the only decay mode (its partial half-life for this decay branch) is the surprisingly long time of 17 s.
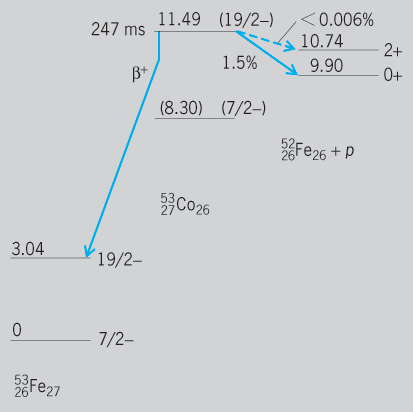
The first two cases of ground-state proton radioactivities were reported in 1982. These were 151Lu → 15070Yb + p (T1/2 = 85 ms) and 14769Tm → 14668Er + p (T1/2 = 0.56 s) produced in the reactions 58Ni + 96Ru and 58Ni + 92Mo. Others were since found as heavy-ion experiments have reached isotopes still further off stability, for example, 11355Cs. Nevertheless, the windows for the observation of direct proton decays are small and, therefore, such decays are very difficult to identify.
As one continues to remove neutrons from the nucleus of a given element with atomic number Z, one reaches a point, called the proton drip line, where for that Z and N a single proton becomes unbound and can drip off the nucleus. The Coulomb barrier (discussed earlier for alpha decay) and the centrifugal (angular momentum) barrier can hold the proton in for a limited time, so the nucleus undergoes radioactive decay with a certain half-life for the emission of a proton. Studies of proton radioactivities probe the limits of stability of proton-rich nuclei. Beyond the proton drip line, proton radioactivity is 100% of the decay. As one moves inside the line to more stable nuclei, proton radioactivity competes with positron decay, and, with the addition of more neutrons, positron beta decay becomes 100% of the radioactivity.
There are numerous examples of proton radioactivities with half-lives from hundreds of milliseconds down to microseconds. Most proton radioactivities have Z between 63 and 82, and most of these proton-radioactive nuclei are spherical. However, an example of proton radioactivity has been found for well-deformed 131Eu, which decays by proton emission to 130Sm, which is likewise well-deformed. Fine structure in the proton spectrum is observed with decays to the ground and first excited states of 130Sm to establish the large deformation of this nucleus. Proton fine-structure radioactivities have been observed both in the 146Tm ground state and from an isomeric state 146mTm (Fig. 14).
Proton radioactivities make it possible to probe the structure of nuclei at the limits and beyond the limits of stability. The half-lives for proton decays are strongly dependent on the energies of the proton and on the angular momentum carried away by the proton. Proton emitters are odd-Z nuclei because in such nuclei the energy to break apart a proton pair in the nucleus is not needed for proton emission to occur. The angular momentum carried away by the proton gives insight into which orbit the proton occupied prior to emission. Moreover, studies in which the proton emission has been used to tag the recoils of a heavy-ion reaction after mass separation have allowed the observation of the gamma rays emitted by the recoil nucleus prior to proton emission Tm (Fig. 14). Thus, it is possible to study excited states in nuclei beyond the limits of proton stability. Both such data test theories of nuclear structure under new extreme conditions. In addition, the energies of the protons provide information about the mass differences of nuclei at the drip lines and so probe mass formulas out to new limits as well.
Two-proton radioactivities from ground states of nuclei have also been observed including the decay of 45Fe, 4526Fe → 4324Cr + 2p, as well as the two-proton decay of an excited state in 18Ne to 16O.
Neutron radioactivity
In very neutron-rich nuclei near the boundary line of nucleus stability, one may find nuclei with ground or excited states which are unstable to the emission of one or two neutrons. Here, there is no Coulomb barrier to hold the neutron in the nucleus, but one can have a centrifugal barrier that may give rise to one- or even two-neutron radioactivity. These processes for ground states would be very near the limits where nuclei become totally unstable to the addition of a neutron, the neutron drip line, and very difficult to even make much less measure. However, there may be neutron-rich nuclei with high spin isomeric states where the high spin analogous to the one in 53mCo gives rise to a large centrifugal barrier. Such isomeric states may undergo one- or two-neutron radioactivity.
Delayed particle emissions
Many types of beta-delayed particle emissions have been observed (Table 1). Theoretically, the number of isotopes which can undergo beta-delayed particle emission could exceed 1000. Thus, this mode is among the important ones in nuclei very far from the stable ones in nature. Studies of these decays can provide insights into the nucleus which can be gained in no other way.
Beta-delayed alpha radioactivity
The β− decay of 214Bi to 214Po leaves the nucleus in such a high-energy excited state that it can emit an alpha particle and go to 210Pb as an alternative to gamma-ray decay to lower levels in 214Po. This is a two-step process with beta decay the first step. After beta decay, the nucleus is in such a highly excited state that it can emit either an alpha particle or gamma ray.
The β− delayed alpha emission has been found relatively rarely, but in many cases beta (β+, EC) delayed alpha emission has been discovered. In proton-rich nuclei far from stability, the conditions are more favorable for beta (β+, EC) delayed alpha emission because of the excess of nuclear charge, and a number of such beta-delayed alpha emitters are now known.
Beta-delayed neutron radioactivity
In 1939, shortly after the discovery of nuclear fission, it was proposed that the delayed neutrons observed following fission were in fact beta-delayed neutrons. That is, after the nucleus fissioned, the beta decay of the neutron-rich fission fragments populated high-energy excited states that could promptly undergo dual decay, emitting either a gamma ray or neutron. The processes of beta-delayed two- and three-neutron emission were discovered in 1979 and 1980 in the decay of 11Li, and β−2n to 4n decays were subsequently observed in other nuclei.
The process of beta-delayed neutron emission is essential for the control of nuclear fission reactors. When neutrons absorbed by 235U cause the 236U nucleus formed to fission, many of the fission products undergo beta-delayed neutron emission. These neutrons are important in producing more fission events. In a nuclear reactor, the rate of neutron-induced fission must be controlled to prevent the fission reactions from running away and destroying the reactor. The rate of fission depends on the number of neutrons available. The numbers of neutrons can be controlled by moving in and out of the reactor control rods, which contain material with very high neutron absorption rates. Because many of the neutrons emitted in fission are delayed by beta-decay half-lives, these half-lives allow time for the control rods to be mechanically inserted and removed to control the rate of fission. See also: Delayed neutron
Beta-delayed proton radioactivities
In addition to proton radioactivity, one can have beta-delayed proton and beta-delayed two-proton radioactivities, which again ultimately result in emission of protons from the nucleus. These latter processes also occur in quite proton-rich nuclei with very high decay energies; however, they are complex two-step decay modes whose fundamental first step is beta decay.
Dozens of nuclei ranging from 96C to 18380Hg have been identified to decay by the two-step mode of beta-delayed proton radioactivity. Typical is the decay of 3318Ar (Fig. 15), with a half-life of 173 ms; it was produced by the 3216S + 32He → 3318Ar + 2n reaction. This isotope decays by superallowed and allowed β+ decay to a number of levels in its daughter nucleus 3317Cl, which immediately (in less than 10−17 s) breaks up into 3216S and a proton. More than 30 proton groups arising from the decay of 3318Ar are observed, ranging in energy from 1 to approximately 6 MeV and varying in intensity over four orders of magnitude. Although it is normally very difficult to study many β-decay branches in the decay of a particular nuclide—because of the continuous nature of the energy spectrum of the emitted beta particles—it is possible to do so when investigating beta-delayed proton emitters. The observed proton group energies and intensities can be correlated with the levels fed in the preceding beta decay and their transition rates, thereby permitting sensitive tests via beta decay of nuclear wave functions arising from different models of the nucleus. β+-delayed two-proton decay has also been discovered, as well as β−-delayed deuteron and triton decay.
Beta-delayed spontaneous fission
There are also observed beta-decay processes where the excited nucleus following beta decay has a probability of undergoing spontaneous fission rather than gamma-ray decay. This is the same process as in spontaneous or isomeric spontaneous fission. The excitation energy of the nuclear level provides the extra energy to make fission possible. The nucleus splits into two nearly equal fragments plus some neutrons. This process is like isomeric spontaneous fission except that the lifetime of the nuclear level is so short that the level would not normally be called an isomer.





